数学@ふたば保管庫 [戻る]
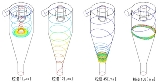
|
数式解いた結果がスレ画だと思うけど、何が言いたいの? |
|
それが正しいとは限らない 落とした葉っぱをどこに落ちるか計算しなさいくらい難しい |
|
宿題は自分でやりましょうね |
|
5個あったお菓子のふたつを食べてしまった 子供は3人 妻もそのお菓子が大好き 俺が来週生きている確率は? |
|
これは良問題 |
|
n + [(n - 1) / 3] + 1 |
|
(4n+1)/3 |
|
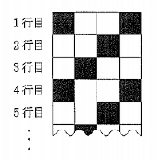
意外と難しいな |
|
n行目になりうる行は2,5,8,11.... またk番目の左から3番目に黒タイルがくる行を考えると n=3k-1 ① と表せる。 「左から3番目に黒タイルがくる行」までのタイルの枚数をxとする xは3,3+4,4+4*2,3+4*3..... と増えていくので x=4k-1 ② ②のkに①を代入すると x=(4n+1)/3 |
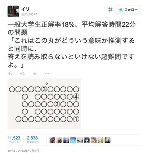
|
高速ヤキソバ変換ちゃん涙目 |
|
ぱっと見1秒であいうえお表だと分かった |
|
1秒は嘘だな 君は話を盛るクセがあるな |
|
>ぱっと見1秒であいうえお表だと分かった 左右弱だったら俺も解かったろうけどねぇ パッと見て1秒で解るのは凄いのかキチなのか |
|
最初見て1分ほど考えて諦めた。 一度寝て、朝目が醒めたときに布団の中でまた少し考えて、五十音表だと気がついた。 寝てる間にヒントが得られてたのかも? |
|
俺も1秒くらいであいうえお表だと思った。 左側の丸の数を詳しく数えて確信に至るまでは10秒ぐらいかな。 |
|
子供の頃からずっとあいうえお表が部屋の壁に貼ってある俺なら1秒 |
|
1,2,3,4は単なる設問か なんか意味があるのかと思った |
|
子供の頃よく見たか見なかったかだな |
|
正解率云々はtwitterにありがちな釣り文句でしょ それを餌に一生懸命考えさせて答えがくだらん下ネタ |
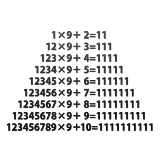
|
パズル的要素 専攻じゃないからな |
|
人生に美を彩り感じるためだよ それ以外に何があるといふのかね? |
|
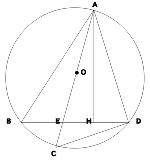
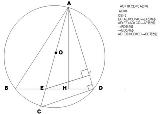
半角の公式使うしかない? |
 たぶんあってる つかれたねる |
|
BE=x,ED=2yとするとAB=3x AH^2=9x^2-(x+y)^2=64-y^2 また2:2y=x:8よりxy=8 上の式に代入してx=√10 |
|
三角形△ABH と 三角形△ACDで、弧ADに対する円周角は等しいので、角∠ABH = 角∠ACD 問題文より、角∠AHB = 90° 半円の弧に対する円周角は 90° になるので、 角∠ADC = 90° 以上より 角∠AHB = 角∠ADC よって、2組の角がそれぞれ等しいので、 三角形△ABH ∽相似 三角形△ACD となる。角∠ADC は直角である。 三角形△ACD は直角三角形なので、三平方の定理により AD = 8 (cm) 角∠EAH = 角∠DAH より 三角形△AED は二等辺三角形なので AE = AD = 8 (cm)ところで、三角形△ADH は直角三角形なので 角∠DAH + 角∠ADH = 90° 一方 角∠ADH + 角∠BDC = 90° なので 角∠DAH = 角∠BDC 円周角は等しいから 角∠BDC = 角∠BAC これらから 三角形△ABH で 角∠BAE = 角∠EAH となり、辺AE は角の二等分線となるから BE : EH = AB : AH = AC : AD = 10 : 8 = 5 : 4 そこで BE = 5x とすれば EH = 4x で BH = 9x となる。 BH : AH = CD : AD = 6 : 8 = 3 : 4 だから AH = 12x 三角形△AEH は直角三角形で AE = 8 , EH = 4x , AH = 12x だから、三平方の定理で x が求まり、BE が求まる。 |
|
なるほどね 解き方もいろいろだが √10だ |
|
こねくりまわしても√10 すっと答えても√10だ |
|
>つかれた >ねる >三角形△ACD は直角三角形なので、三平方の定理により AD = 8 (cm) >角∠EAH = 角∠DAH より 三角形△AED は二等辺三角形なので AE = AD = 8 (cm)ところで、三角形△ADH は直角三角形なので 角∠DAH + 角∠ADH = 90° >一方 角∠ADH + 角∠BDC = 90° なので 角∠DAH = 角∠BDC >円周角は等しいから 角∠BDC = 角∠BAC >これらから 三角形△ABH で 角∠BAE = 角∠EAH となり、辺AE は角の二等分線となるから >BE : EH = AB : AH = AC : AD = 10 : 8 = 5 : 4 >そこで BE = 5x とすれば EH = 4x で BH = 9x となる。 >BH : AH = CD : AD = 6 : 8 = 3 : 4 だから AH = 12x >三角形△AEH は直角三角形で AE = 8 , EH = 4x , AH = 12x だから、三平方の定理で x が求まり、BE が求まる。 よく頑張ったな。 まあつまり答えは√10なワケだ |
|
良問題ありがとう 楽しかった |
|
平成25年度岐阜県 数学 超難問(正答率0%) http://www.5kaku.net/?p=6344 |
|
超難関とは思えないなー 相似と三平方の定理を使えば出てくる。 正答率が0とは岐阜県はお馬鹿ちゃんばかりなのだな 大阪公立前期の文理科を受験する子なら殆どが10分 以内に答えを出せるレベルだよ。 |

|
青函、津軽、函館のふりがなが必要な方たちに、青森駅から船に乗れるかどうかの知識はない 俺もしらない |
|
午前10時10分 |
|
今は知らんが、あずさの偶数号は松本発の上りしかなかった。 |
|
文章に無駄がありすぎるし駅から船まで何分歩いたのかわからないので答えようがない |
|
あずさは青森行かねえだろいい加減にしろ |
|
演歌の歌詞やタイトルが含まれている出題文 出題者はそうとう年配なのかな |
|
>5時間50分後に函館につきました 当時の連絡船の所要時間は 4時間10分なので、なにかトラブルがあったに違いない |
|
何時ついたかって? 15年前だよ |

|
はあ・・・なんちゅう説明の下手糞な奴かね? まずその実数値のとり得る範囲は何かね? 負の無限大から性の無限大までかね? そもそも挙げておる例は自然数のようだが? |
|
とりあえずスレあきの言ってることワケわかめなので、もっとシンプルに問題文を変えてみたぞよ 自然数を出力する完全な乱数生成器がある 今、これを使った乱数の生成を連続的に有限回反復試行するとしよう 反復の最終回の値をできるだけ大きくするには何回目で止めればよいか? これだけでイナフではないかね? 不備があれば指摘したまへ |
|
秘書問題の亜種? 勘では何回目に終了しても期待値は変わらなそうだな |
|
亜種ではなくそのものじゃねえの |
|
1/e |
|
スレッドを立てた人によって削除されました |
|
トランプのカードみたいに用意されてる数が決まっていて 同じ数字が2度でない仕様にすれば 履歴を取る意味もあるし それを利用したn回にも意味もある |
|
スレッドを立てた人によって削除されました |
|
スレッドを立てた人によって削除されました |
|
スレッドを立てた人によって削除されました |

|
2^xを文字で置き換えて、下はヘロンかな? |
|
9と2の間の点は何なの? |
|
掛け算じゃない? |
|
1~4へろ~ん(もしくはAからBCに垂線おろしてその長さをhと置いて三平方定理で等式作ってhを求める) |
|
角AMLが直角ならALは円の直径で ANに直線引いたら角ANLは直角だよな。 てゆうか、面積求めんのに円要らないよな。 引っ掛け? |
|
だから、 3辺の長さがわかれば、 それ以外何もわからなくても面積求めれるってば・・・ |
|
無駄な補助線ほど見ててイライラするものも無い |
|
馬鹿どもにはちょうどいいめくらましだ |
|
ヘロンの公式を知らない学年の問題なんじゃない? |
 本文無し |

|
>数学の才能とは アメリカのトップ機関に入れる事 |
|
>No.95480 自分だと気づいたんだね ご苦労さん |
|
忍耐力馬鹿が必死のご登場ですか |
|
自演がバレたNo.95474でNo.95479が今度は連投で火病w |
|
>自分だと気づいたんだね このレスした人って誰かねw |
|
一人の忍耐力馬鹿が必死になってるのはわかる。 |
|
今頃自己紹介? |
|
すぐ必死になる 必死と言われて言い返さずに入れない もういいってば 誰も忍耐力が必要だなんて思ってないのだから |
|
妥当性に似つかわしくないスレの長さのようなもの |
|
才能があるかどうか簡単な判断方法を教えてやるよ 数式を見ていて眠くなったら才能ない |

|
>No.95334 見慣れないだけでごく自然なこと |
 指の数が両手合わせて16本だったらよかったのに。 |
|
2進法なら、両手で1023まで数えられますよっと |
|
2進換算なら、 16進数は指4本で一桁、両手で最低でも2桁は数えたり計算できたりする。 8進数は指3本で一桁、両手で最低でも3桁は数えたり計算できたりする。 10進数は厳しいな。 |
|
>1023 |
|
俺は左手1本で万年カレンダー出来るよ 年月日から曜日算出もほんの数秒程度 |
|
>2進法なら、両手で1023まで数えられますよっと ためしにやってみたら指が痛くなった 駄目だこりゃ |
|
12でグワシ |
|
神様ハ、人間ガ直グニ二進数ニ辿リツカナイ様ニ、指ヲ10本ニシタ。 掴ムダケナラ、二本デ充分ナノニ。 |
|
二本指で生活してみろ |
| [0] [1] [2] [3] [4] [5] |