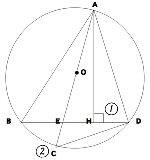
>媮傔傗偑傟丅
偦偺傑偊偵嘆偵捈妏儅乕僋擖傟傗偑傟嘇偑墌O 偺廃忋偵偹乕偧
悢妛仐傆偨偽曐娗屔 [栠傞]
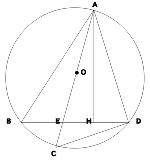
 >媮傔傗偑傟丅 偦偺傑偊偵嘆偵捈妏儅乕僋擖傟傗偑傟嘇偑墌O 偺廃忋偵偹乕偧 |
|
嶌恾偼僟儊偩偑愢柧偩偗偼偟偭偐傝偟偰傞偺側 |
|
愢柧偑偟偭偐傝偟偰傞偺偼摉偨傝慜偱嶌夋偑僟儊側偺傪尒摝偡恄宱偑僉儌偄 |
|
夝偗側偄搝偼暥嬪偑懡偄 |
|
併10 |
|
>BE 偺挿偝傪媮傔傗偑傟丅 偙偆偄偆僙儞僗偼岲偒偩 |
|
併10 |
|
併10 |
 杮暥柍偟 |
|
彂偒崬傒傪偟偨恖偵傛偭偰嶍彍偝傟傑偟偨 |
|
敿妏偺岞幃巊偆偟偐側偄丠 |
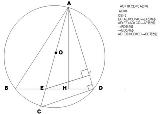 偨傇傫偁偭偰傞 偮偐傟偨偹傞 |
|
BE=x,ED=2y偲偡傞偲AB=3x AH^2=9x^2-(x+y)^2=64-y^2 傑偨2:2y=x:8傛傝xy=8 忋偺幃偵戙擖偟偰x=併10 |
|
嶰妏宍仮ABH 偲 嶰妏宍仮ACD偱丄屖AD偵懳偡傞墌廃妏偼摍偟偄偺偱丄妏佢ABH 亖 妏佢ACD 栤戣暥傛傝丄妏佢AHB 亖 90亱 敿墌偺屖偵懳偡傞墌廃妏偼 90亱 偵側傞偺偱丄 妏佢ADC 亖 90亱 埲忋傛傝 妏佢AHB 亖 妏佢ADC 傛偭偰丄俀慻偺妏偑偦傟偧傟摍偟偄偺偱丄 嶰妏宍仮ABH 佷憡帡 嶰妏宍仮ACD 偲側傞丅妏佢ADC 偼捈妏偱偁傞丅 嶰妏宍仮ACD 偼捈妏嶰妏宍側偺偱丄嶰暯曽偺掕棟偵傛傝丂AD = 8 (cm) 妏佢EAH = 妏佢DAH 傛傝 嶰妏宍仮AED 偼擇摍曈嶰妏宍側偺偱 AE = AD = 8 (cm)偲偙傠偱丄嶰妏宍仮ADH 偼捈妏嶰妏宍側偺偱 妏佢DAH 亄 妏佢ADH = 90亱 堦曽丂妏佢ADH 亄 妏佢BDC = 90亱丂側偺偱丂妏佢DAH = 妏佢BDC 墌廃妏偼摍偟偄偐傜 妏佢BDC = 妏佢BAC 偙傟傜偐傜丂嶰妏宍仮ABH 偱 妏佢BAE = 妏佢EAH 偲側傝丄曈AE 偼妏偺擇摍暘慄偲側傞偐傜 BE : EH = AB : AH = AC : AD = 10 : 8 = 5 : 4 偦偙偱 BE = 5x 偲偡傟偽 EH = 4x 偱 BH = 9x 偲側傞丅 BH : AH = CD : AD = 6 : 8 = 3 : 4 偩偐傜 AH = 12x 嶰妏宍仮AEH 偼捈妏嶰妏宍偱 AE = 8 , EH = 4x , AH = 12x 偩偐傜丄嶰暯曽偺掕棟偱 x 偑媮傑傝丄BE 偑媮傑傞丅 |
|
側傞傎偳偹 夝偒曽傕偄傠偄傠偩偑丂併10偩 |
|
偙偹偔傝傑傢偟偰傕併10 偡偭偲摎偊偰傕併10偩 |
|
>偮偐傟偨 >偹傞 >嶰妏宍仮ACD 偼捈妏嶰妏宍側偺偱丄嶰暯曽偺掕棟偵傛傝丂AD = 8 (cm) >妏佢EAH = 妏佢DAH 傛傝 嶰妏宍仮AED 偼擇摍曈嶰妏宍側偺偱 AE = AD = 8 (cm)偲偙傠偱丄嶰妏宍仮ADH 偼捈妏嶰妏宍側偺偱 妏佢DAH 亄 妏佢ADH = 90亱 >堦曽丂妏佢ADH 亄 妏佢BDC = 90亱丂側偺偱丂妏佢DAH = 妏佢BDC >墌廃妏偼摍偟偄偐傜 妏佢BDC = 妏佢BAC >偙傟傜偐傜丂嶰妏宍仮ABH 偱 妏佢BAE = 妏佢EAH 偲側傝丄曈AE 偼妏偺擇摍暘慄偲側傞偐傜 >BE : EH = AB : AH = AC : AD = 10 : 8 = 5 : 4 >偦偙偱 BE = 5x 偲偡傟偽 EH = 4x 偱 BH = 9x 偲側傞丅 >BH : AH = CD : AD = 6 : 8 = 3 : 4 偩偐傜 AH = 12x >嶰妏宍仮AEH 偼捈妏嶰妏宍偱 AE = 8 , EH = 4x , AH = 12x 偩偐傜丄嶰暯曽偺掕棟偱 x 偑媮傑傝丄BE 偑媮傑傞丅 傛偔婃挘偭偨側丅 傑偁偮傑傝摎偊偼併10側儚働偩 |
|
椙栤戣偁傝偑偲偆 妝偟偐偭偨 |
|
暯惉25擭搙婒晫導丂悢妛丂挻擄栤(惓摎棪0%) http://www.5kaku.net/?p=6344 |
|
挻擄娭偲偼巚偊側偄側乕 憡帡偲嶰暯曽偺掕棟傪巊偊偽弌偰偔傞丅 惓摎棪偑侽偲偼婒晫導偼偍攏幁偪傖傫偽偐傝側偺偩側 戝嶃岞棫慜婜偺暥棟壢傪庴尡偡傞巕側傜杦偳偑侾侽暘 埲撪偵摎偊傪弌偣傞儗儀儖偩傛丅 |