数学@ふたば保管庫 [戻る]

|
562,300円あたり? |

|
-1*1 =-1 =-(1*1) =-(1)^2 |
|
小学生からやり直せ |
|
1+1=田 |
|
題名使ってる初心者久しぶりに見た |
|
>題名使ってる初心者久しぶりに見た 久しぶりがどれくらいなのか知らないけど スレ画は3〜4週間前にも「数学を超越した」とかなんとか言って スレ立ててたぞい |
|
バナッハ=タルスキーの パラドックスとか |
|
チャイティンの定数とかはどうかな? 確かに存在しているのに 計算は原理的に不可能っていう |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
たとえば古典論理で(背理法を使えば)∃x P(x) を証明できるが、 直感主義論理での証明を構成できないケースとかが 当てはまるんジャネ 具体例は知らん 背理法のシークエント計算をよく見れば何か見出せるかも試練、 見出せたならそれは推論規則を古典論理に固定した下でも背理法で証明するしかない述語ということで、スレの題意を満たす 、希ガス |
|
Rを実数全体の集合とする。 Sを「具体的に構成可能」なRの部分集合の全体とする。 Sの補集合が空でないことを証明可能であるなら、 P(x)を「xはSに含まれない」とすれば良い。 問題は「具体的に構成可能」とは何を意味するのかということだが…。 |
|
「具体的に構成可能」が「有限回の手続きで構成可能」を意味するとしたとき、 Sは明らかに可算集合になる。 Rの部分集合の全体は非可算なので、 Sの補集合は空ではない。 ということで、P(x)として「xはSに含まれない」とすれば良い。 |
|
変域指定なしで集合定義するとかダメだろそれ まあPAとか不完全なモデル構成すればよろしい |

|
6) 2 * [ 10 * ( π*10^(n-2)-[π*10^(n-2)] ) ] []は床関数 |
|
↑ むっ!目眩ましか! |
|
>No.95301 そうですね。sin(nπ/2)ですね。別件で2進数で頭がいっぱいだったので、腐ってた。 同じように 5)は cos(2(n-1)π/3)+isin(2(n-1)π/3)=e^(2/3)(n-1)πi |
|
書き込みをした人によって削除されました |
|
ていうか所与のn項{ a_1, a_2, ..., a_n }が一致するだけで良いならそのような数列は解析的な解を機械的に求めることができ(ry しかも候補は無数にある(具体的に見出せる)たとえばデータ点列(1, a_1), (2, a_2), ..., (n, a_n)にフィッティングするn-1次以上の多項式(の係数)を最小二乗法か何かで求めるとか、 |
|
はぁ・・・ |
|
6)に規則性なんかない。 円周率の各桁を2倍にしただけ。 |
|
>円周率の各桁を2倍にしただけ。 そこをなんとかお前のコスイ頭で式として求めんかい! |
|
2π |
|
>高速ヤキソバ変換 おまえ五月蠅いよ |

|
偶奇とは関係ないけど無限とは関係有るんじゃない? |
|
有限で成り立つからって無限でも成り立つとは限らないって事でしょ。 無限は怖いんだから・・・ |
|
1×1×1×…=1 は正しいのだろうか? 1×1×1×…=3.14159... とかなってたらステキ |
|
>>πをかければ整数ですらないが > >言い方が悪かった >上の問題の話について それでも間違ってるぞ |
|
>それでも間違ってるぞ どこが間違ってるか教えて欲しい |
|
お前ら知ってるか?無限大は自然数じゃ無いんだぜ! |
|
ここは基本に戻ってコーシーの増大列でもって 素数の積の無限大というものを定義しようではないか すなわちNを自然数の集合、P(k)を第k項までの素数の積とすれば ∀n∈N ∃m∈N P(m) > n が成り立つ このP(m)こそはあきらかに自然数であり偶数であり しかも同時に無限大であることを示している ビバ!コーシー!ありがとう!コーシー!ドトール!コーシー! |
|
いみなし |
|
いやだからー1は素数では無いが 2は素数なのですよ。お仕舞い |
|
人数合わせで仕方なく高速ヤキソバ変換みたいなのを呼んだ経験あり 最悪だったわ |
|
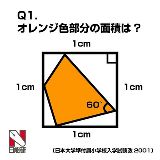
有名な釣り画像貼ってんじゃねーよボケ sageとこ |
|
幼稚園で分数・小数マスターしてないと小学校入れないのか |
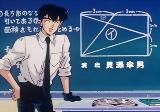 じゃあこっちで |
|
計算ではなく、図形計測的アプローチによると
0.509cm^2 |
|
間違いなく、1/2㎠です。 60°の頂点を一辺の中点に 持ってくればお仕舞いですね。 |
|
頂点動かしたら面積変わるやろ |
 1/2cm2では断じてないな |
|
日本大学準附属小学校か 毎年良い問題出すという定評があるよね |
|
園児向けとして良い問題なの? |
|
日本大学準附属小学校とか存在しないから。 |

|
{r|r∈R,x∈N,y∈N,z∈N,x^r+y^r=z^r}ってどんな集合なんだろう (便宜上Nは0を含まないってことで) |
|
>{r|r∈R,x∈N,y∈N,z∈N,x^r+y^r=z^r}ってどんな集合なんだろう それ考えるとどんないいことがありますか? |
|
>>{r|r∈R,x∈N,y∈N,z∈N,x^r+y^r=z^r}ってどんな集合なんだろう >それ考えるとどんないいことがありますか? 知らん 自然数の範囲でそれを調べるのがものすごく難しい問題だったのだから 実数の範囲ならどうなるんだろうというただの思いつきだから |
|
実数じゃなくて有理数だとどうなん? |
|
スレッドを立てた人によって削除されました |
|
有理数でも反例ありそう 頭いい人に任せる |
|
x、y、zが有理数としてその公倍数をaとすると 両辺にa^nをかけるとそれぞれは自然数になるから解は存在しない |
|
つ、釣られないぞ… |
|
書き込みをした人によって削除されました |
|
ようわからんがnが有理数だったら?という問いなのでは… 互いに素な自然数p, qを使ってn=p/qとおく。 まず、x,y,zがある自然数u, v, wのq乗なら3以上の自然数pについて u^p + v^p = w^pを満たす自然数u,v,wが存在するかという問いに帰着し、そのような自然数u,v,wは存在しない。 x,y,zの中にある自然数のq乗でないものが含まれるなら、x^(p/q)+y^(p/q)=z^(p/q)の3項のどれかは無理数。 いま((x^p)/(z^p))^(1/q) + ((y^p)/(z^p))^(1/q) = 1、 さらに (x^p)/(z^p) = ( 1 - ((y^p)/(z^p))^(1/q) )^q と変形したとき、仮にyかzが(自然数)^qでないなら、右辺は(無理数)^qで、かつq乗した結果も無理数。 (y=zはこの場合有り得ない)故に左辺は有理数では有り得ず、x, zが同時に自然数では有り得ない。 xとyを取り替えて同じ論法に従えば、xかzが(自然数)^qでないなら、yとzが同時に自然数では有り得ない 結局x,y,zの中にある自然数のq乗でないものが含まれるなら、x, y, zの中に、同時に自然数では有り得ない2組が生じる 、希ガス |

|
最小は8個だよ 縦横に半分ずつ斬ってそこから2個取るのだよ 残りの不要な6個の羊羹は私が頂く |
|
こっちも12ピース http://www.nicovideo.jp/watch/sm16680839 |
|
難しいな・・・ |
|
難しすぎてこの掲示板にはそぐわない! |
|
いえーいピースピース |
|
仮に最少のピース数が12だったとして そのことをどうやって証明するのか。 11ピース以下のありとあらゆる分割を網羅して 2個の立方体に組み立てられないことを 証明せよとでもいうのか。 |
|
そういうときは"数学"を使うんだよ |
|
>>94911 どういう数学を使えばいいんでしょうか? |
|
>最小は8個だよ >縦横に半分ずつ斬ってそこから2個取るのだよ >残りの不要な6個の羊羹は私が頂く その方法なら最少3個だろ |

|
グロタンディーク亡くなったのですか |
|
つか、死亡記事見てまだ生きてたんだとオモタ |

|
A-BCDE:A-BCPQ = ACD:ACP |
|
粘土で作って実測 |
|
>No.95068 違うよ |
|
ABCQ=(6/9)*ABCE APCQ=(6/9)*(6/9)*ACDE 5/9 |
|
有り難う御座いました。素晴らしい解答です。 今日、授業があるそうなので早速教えてやります。感謝 自分でも無理矢理計算してA-BCPQの体積を20√7まで 出していましたが、あなたのやり方の方が数段説得力が あり美しいです。有り難う御座いました。 |
|
歯が立ちませんと書いておきながら20√7まで 出していました? 初めからエレガントな解き方が聞きたいならそう言え あとなあ、息子の塾の宿題なんて嘘をつくな 二度と書き込むなよゴミ野郎 |
|
最近よく見かけるが小中学生の宿題を聞く輩は塾講師かカテキョでしょう 解けないと食いっ逸れるんだろうよ |
|
息子の宿題で親が苦労するとか、 塾の意味なくね? 宿題だからといっても、 わからない問題は解けなくて当然なのだから、 塾で出された問題は塾で聞くのが一番だろう。 |
|
95076,95077の言うとおりだな。塾講師なら自分で解けよ。 BCの長さは与えられなくても体積の比はでるねえ。 |
|
塾へいけばいい |
| [0] [1] [2] [3] [4] [5] |