数学@ふたば保管庫 [戻る]

|
アラビア数字がいかに偉大な発明で在ったかが よく分かるな |
|
>アラビア数字がいかに偉大な発明で在ったか 痛感します |
|
というか位取り記数法の利便性 |
|
だけど本当に偉大なのは演算記号だろう。 |
 アラビア数字がそれどほ無理なく7セグメントで表現できるというのは、偶然なんだろうけど人類にとってすごい幸運だと思う。 |
|
4セグメントあればそれどほ無理なく13種類まで判別できる事を考えたら 7セグメントが果たして幸運かどうかは何とも言えなくね? |
|
アンラッキー
漢数字のセグメント表示を考えてみましたが、 かなり無理しても14セグメント必要な感じ。 |
 ゼビ数字、 |
|
>漢数字のセグメント表示を考えてみましたが、 >かなり無理しても14セグメント必要な感じ。 面白いな 六を諦めれば上の一つはけずれそう |
|
10進数とかマジ勘弁 なんで12進数か16進数にしなかったの |
|
10進数のどこがいかんとですか? |
|
>というか位取り記数法の利便性 なにが「というか」なんだ? |
|
>10進数とかマジ勘弁 >なんで12進数か16進数にしなかったの 人類の手の指の数が10本だったから (桁という意味の"digit"はラテン語の「指」が由来) >10進数のどこがいかんとですか? 約数が少ない(1と自身の数を除くと2と5しかない) 12なら2と3と5 16なら2と4と8の他に整数の平方根と立方根を持つ |
|
No.95106 ミス 誤:12なら2と3と5 正:12なら2と3と6 |
|
>10進数のどこがいかんとですか? 2進数に変換しにくいのも問題と言えるかも。 この場合8進数や16進数が有利だね。 |
|
16進数最強だろうね。 整数の平方根と立方根を持つというのは コンピュータの世界でも非常に区切りがよいし有用。 プログラミングだと10進数は極めて半端に感じる。 |
|
まあ、電子回路がHi、lowの2進数だから、 メモリ素子から何から何まで2の倍数。 もし16進数の数字があって、 それで計算するのが当たり前の世界なら、 今より効率の良い便利な公式が編み出されてただろうかね。 |
|
アセンブラでいうところのbitシフトやローテトが使えるね |
|
9進や11進といった奇数進数の不都合な点は? 半分に割り切れないというのはすぐに思いつくけど、他にもあるかな? |
|
>9進や11進といった奇数進数の不都合な点は? 半分に割り切れないと思ってる人が居るって事かな |
|
365進数は、4年に一回366進数にしなきゃいけなくて不都合だよな! |
|
>>9進や11進といった奇数進数の不都合な点は? >半分に割り切れないと思ってる人が居るって事かな 実際10(9)や10(11)は2で割り切れないぞ |
|
>実際10(9)や10(11)は2で割り切れないぞ 久しぶりにこんな時間に覗きに来たのにこんな馬鹿に遭遇しちゃった |
|
いやあってるだろ |
|
煽るだけの脳なしの相手すんなボケ sage |
|
>No.95106 >ミス >誤:12なら2と3と5 >正:12なら2と3と6 それミソらせたまへ 16進数ではこんな簡単なことですらミス間違いをお菓子安いではないか やはり10進数が一番妥当なのだよ |
|
>16進数最強だろうね。 >整数の平方根と立方根を持つというのは >コンピュータの世界でも非常に区切りがよいし有用。 10進数でも整数の平方根と立方根を持ち得ますが? だいたい根をもってコンピュータで区切りがよいとは何のこっちゃかね? |
|
>16進数ではこんな簡単なことですらミス間違いをお菓子安いではないか 10進法で背爪石てる身体よ 123456789*☆‖〇Д□↓ならミス間違いをお菓子たりは竹刀 |
|
高速ヤキソバ変換 お前マジで気付いてないのか? |
|
来年の正月問題 720の約数は 何個あるか そのうち5の倍数は何個あるか 5の倍数の合計はいくつか |
|
ウィキペディアより
720 は合成数であり、約数は1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 30, 36, 40, 45, 48, 60, 72, 80, 90, 120, 144, 180, 240, 360 と 720 である。 12番目の高度合成数であり、約数を30個持つ。一つ前は360、次は840。 14番目の高度トーティエント数である。一つ前は576、次は1152。 6番目の階乗数6!である。一つ前は120、次は5040。 |
|
書き込みをした人によって削除されました |
|
やっぱ人たるもの日常生活において 2等分と3等分と4等分ぐらいには対応したい しかし5等分とか6等分とか7等分とかが必要かといわれるとビミョー というわけで12個ひとまとめにして売ったり買ったりするいうのはなかなか具合が良い よって物事ダース単位で数えるし、 時計は(というか角度は)1周が12の倍数で等分されあるようになった 希ガス、、 |
|
>やっぱ人たるもの え?人だったの?カスだと思ってたよ |
|
円周を360等分して1度としてるのはいろいろと具合良いよね。 |
|
10進数以外をメインに使ってた文明って全く存在しなかったのだろうか |
|
>10進数以外をメインに使ってた文明って全く存在しなかったのだろうか インダス文明では2進数が日常的に使われていた |
|
コンピュターが2進法なのは電気がONとOFFだからでしゅ インダス文明が2進法だったのは、各桁を構成する数値で一番小さい数字が1だったからで、より少ない分銅で測ろうとすれば、計量の基数が1になる事はしょんなに驚く事実ではありましぇん しゅかも分銅は、128までは2進行の比率でしゅが160から32000までは10進法の比率でしゅた 初期の数え方で言うと原始人は無い・有る・沢山の3進法を使っていましゅた 1ビットの2進法と見做すだけなら中国の陰陽も一種の2進法でしゅし、八卦・六十四卦もそれぞれ3ビット・6ビットの2進数でしゅ しゅかしこれらは二種の値の組を辞書式順序に並べただけで計算には用いられていましぇんでした |
|
1・2・3・4・5・6・7・8・9は、和語数詞では、ひと・ふた・み・よ・いつ・む・なな・や・ここの、になりましゅ これをローマ字表記しゅるとHito・huta・mi・yo・itu・mu・nana・ya・kokono、になりましゅ 1hitoの2倍は2huta 3miの2倍は6mu 4yoの2倍は8ya の様に母音が他の母音に変化しゅると数値が2倍に 改良2進法でしゅ |
|
>1hitoの2倍は2huta 3miの2倍は6mu 4yoの2倍は8ya 2の2倍は? |
|
>だいたい根をもってコンピュータで区切りがよいとは何のこっちゃかね? まず、16進数は1桁4bit固定なので変換が容易い。 たとえば電卓の回路を自分で設計もしくは仕組みを調べればわかるが、10進数を扱うというのとても効率が悪いのだ。 それに必要なメモリ素子は2^nでちょうど無駄なく区切りがよい。それはビットマップに展開しても同じで、たとえばスクロールさせようと思ったら、ビットシフトだけで事足りるんだよ。 |
|
てか、ビットシフトは2倍ね。 2進数は2倍するとビットが左に1桁ずれる。 16進数だと4ビットずらせばシフトする。 |
|
>2進数は2倍するとビットが左に1桁ずれる。 >16進数だと4ビットずらせばシフトする。 p進数はp倍すると左に1桁ずれる。 当たり前じゃね? プログラミングを発端として2進数を覚えると シフト操作が特別なものに思えるかも知れんけど 10進数なら10倍でシフトなので単なる桁上げと同義 |
|
>10進数なら10倍でシフトなので単なる桁上げと同義 10進数でデータ保持されてるコンピュータなんてありませんよ。 それこそ電卓回路と一緒でとても苦労する。 |
|
たとえば、2進数 00001100 2倍するとビットが左にシフトするけど、 16倍すると16進数で一桁左にシフトする。 >10進数なら10倍でシフトなので単なる桁上げと同義 じゃあ、どのようにシフトさせれば10倍になるのか? |
|
>10進数でデータ保持されてるコンピュータなんてありませんよ。 2進数なら2倍でシフトなので単なる桁上げと同義 と書けば伝わるかな 要は「シフト」も「桁上げ/桁下げ」も何進数だろうが同じってことを言いたいだけ 電気/電子回路の実装効率の話は別としてね |
|
コンピュータで区切りがよいとは何のこっちゃかね? という話の流れで、電子回路の実装効率の話は別としてね って何ですかそれ? n進数がn倍で桁が上がるなんて当たり前のことを言われても… |
|
ホントにねぇ No.95146は何を言ってるんだか |
|
>てか、ビットシフトは2倍ね。 >2進数は2倍するとビットが左に1桁ずれる。 >16進数だと4ビットずらせばシフトする。 10進数はビットシフトで桁上げすることが出来ない って言ってるんだよ |
|
つまり合ってるじゃん。 |
|
10進浮動小数点演算ユニットはあるけど、何かいてあるかわかんない http://news.mynavi.jp/column/architecture/105/ |
|
噛みあわんw |
|
浮動小数点演算ユニットは自由に桁が動く10進コンピューターだよ |
|
>No.95173 結局内部は2進数なんだよ。 使わないビット、立つことのないビットがあって 限られた演算でしか使えない。 どちらにしても10進だと DPDとBCDの変換回路、加算器が必要だし 2倍と5倍のための回路も必要だろう 電卓の回路を考えてみればすぐに気付く |
|
日清数がディジタル回路と相性がよいことはわかるのだよ 私が聞きたいのは >整数の平方根と立方根を持つというのは >コンピュータの世界でも非常に区切りがよい 最初からここだよ 整数の根を持つことにディジタル回路の相性の良さと何の関係があるのかね? |
|
電子回路と整数の平方根をもつn進数との相性がいいのは 単純に分割処理しやすいって点だよ |
|
記憶装置の容量、 メモリ容量、 コンピュータの色数、 画面サイズ、 悉く平方根のほうが効率よいね |
|
>整数の平方根をもつn進数 いやだから何進数だろうが整数の平方根は持つますが? それを持たない進数表現があると言うのかね? |
|
>高速ヤキソバ変換 >日清数 ふむ、つまりUFOということか? |
|
>16進数にしなかったの じゅうろくいち、じゅうろくになんて言いたくないから 9の後にAが来るのも理不尽 |
|
>じゅうろくいち、じゅうろくになんて言いたくないから 実際に16進数になったら「じゅうろく」に違和を感じなくなる 言いたくないのは個人の自由 >9の後にAが来るのも理不尽 別に理不尽ではない |
|
9のつぎAにしましょって誰が言いだしたんだろね |
|
7セグメントLEDで、0~9の他に一応A〜Fを表示可能。 このおかげで、ディスプレイとして7セグメントLEDしか持たなかったTK-80とかのワンボードマイコンでも16進数を表示できて便利だった。 |
|
TK-80は買ってもらえなかったなBSも 数年お金ためてやっと買えたのはPC-8001 GAME言語とか知ってる人いるかなあ |
 コンポBS |
|
せめて8進数でもいいんだけど。 3ビットで一桁で当然10進数よりは区切り良い。 |
|
8と9が拗ねる |
|
17を表すに10進数だと17、16進数だと11 形の表現として16進数は納得しづらい さらに8進数だと21になってしまう この世の終末だ! |
|
>No.95334 見慣れないだけでごく自然なこと |
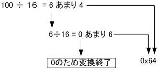 指の数が両手合わせて16本だったらよかったのに。 |
|
2進法なら、両手で1023まで数えられますよっと |
|
2進換算なら、 16進数は指4本で一桁、両手で最低でも2桁は数えたり計算できたりする。 8進数は指3本で一桁、両手で最低でも3桁は数えたり計算できたりする。 10進数は厳しいな。 |
|
>1023 |
|
俺は左手1本で万年カレンダー出来るよ 年月日から曜日算出もほんの数秒程度 |
|
>2進法なら、両手で1023まで数えられますよっと ためしにやってみたら指が痛くなった 駄目だこりゃ |
|
12でグワシ |
|
神様ハ、人間ガ直グニ二進数ニ辿リツカナイ様ニ、指ヲ10本ニシタ。 掴ムダケナラ、二本デ充分ナノニ。 |
|
二本指で生活してみろ |