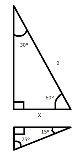
塻妏偑30亱偲60亱偺捈妏嶰妏宍偩偐傜丄
2:X = 2:1 2X = 2 X = 1崅偝偑夝偭偨偐傜柺愊偼 (2*1)/2=1偱ok?
悢妛仐傆偨偽曐娗屔 [栠傞]


|
乽夞揮暔棟妛乿偐丒丒丒 僼僢丒丒丒柺敀偄乽壖愢乿偩側 |
|
係師尦儐乕僋儕僢僪嬻娫偺暔棟偐 偲傝偁偊偢乽帪娫乿偲偄偆摿暿側曽岦偑柍偔側傞偺偱 僄僱儖僊乕偲塣摦検偺嬫暿傕柍偔側傞偟 曐懚検偼儐乕僋儕僢僪僲儖儉偺夞揮懳徧惈傪帩偮傛偆偵側傞偹 |
 塻妏偑30亱偲60亱偺捈妏嶰妏宍偩偐傜丄 2:X = 2:1 2X = 2 X = 1崅偝偑夝偭偨偐傜柺愊偼 (2*1)/2=1偱ok? |
|
http://cgi.2chan.net/m/res/94679.htm |
|
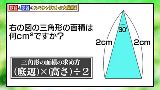
2偮偔偭偮偗偨偨偙宍偺懳妏慄偑堦曈2cm偺惓嶰妏宍偺堦晹偵側偭偰傞偭偰愢柧偡傞偲偍傫側偠傾僾儘乕僠偩偗偳僥儗價塮偊偟偦偆 |
|
亜塻妏偑30亱偲60亱偺捈妏嶰妏宍偩偐傜丄 擇摍曈嶰妏宍偺捀揰偑30亱側偺偵偳偆偟偰偦偆側傞丠丠 |
|
>偳偆偟偰偦偆側傞丠丠 偦偺擇摍曈嶰妏宍偺曅曽偺掙妏偺捀揰偐傜僜儗偺懳曈乮摍曈)傊偺悅慄偑堷偐傟偰丄偦偆側傞丅 |
|
偲傝偁偊偢悅慄堷偄偰捈妏嶰妏宍丅 惓嶰妏宍偺敿暘偩偲巚偭偰傕偄偄偟丄 奜愙墌傪峫偊傞偲捈宎丄敿宎偑尒偊偰偒偰丄丄偲偐傗偭偰傕 |
|
擻椡偲偄偆偐丄拪徾揑巚峫傪挿帪娫偡傞偨傔偵 僗僞儈僫偑偄傞傫偩傛偹 恖娫偺擼偼丄惗壔妛揑僄僱儖僊乕傪戝検徚旓偡傞婍姱偱 庒偄恖偠傖側偄偲戝弌椡偱挿帪娫摦偐偣傞偩偗偺 戙幱棪偑堐帩偱偒側偄偲偄偆棟桼傕偁傞 傑偁丄悢妛偺悽奅偱偼俁侽嵨傑偱偵幚愌傪嫇偘傜傟側偄恖偼 僟儊恖娫偱偡偺偱堷戅偡傞偐嫵堢偵夞傝傑偡 |
|
僗僞儈僫偐 側傞傎偳偹偦偺夝庍偼柍偐偭偨 |
|
係係嵨偱庴尡悢妛傗偭偰傑偡 |
|
>嫵堢偵夞傝傑偡 壗偺偨傔偵丠 |
|
>>嫵堢偵夞傝傑偡 >壗偺偨傔偵丠 栰曢側偙偲傪暦偔側傛 |
|
尋媶幰偼3帪娫偩偐悢妛偺僩儗乕僯儞僌偟偰偐傜尋媶偡傞偲偐暦偄偨偙偲偁傞 偦偺僩儗乕僯儞僌偑偳偆偄偆傕偺偐偼巆擮側偑傜暦偄偰側偄傫偩偗偳 |

|
偹偊摎偊偼丠 寢嬊偔偩傜側偄側偧側偧偩偭偨偺偐 |
|
彂偒崬傒傪偟偨恖偵傛偭偰嶍彍偝傟傑偟偨 |
|
揹抮偺婲揹椡:E 撪晹掞峈:r 揹媴偺掞峈:R 揹抮偺屄悢 :n (n>=2) 夞楬揹棳 捈楍愙懕:Is 暲楍愙懕:Ip 揹媴揹椡 捈楍愙懕:Ps 暲楍愙懕:Pp 偦傟偧傟偺揹椡偼 Ps=R*(Is)^2 Pp=R*(Ip)^2 偱揹棳偺2忔偵斾椺偡傞丅埲壓揹棳偺傒偵拝栚偡傞丅 Is=nE/(nr+R) Ip=E/((r/n)+R)=nE/(r+nR) 暘巕偼 nE 偱嫟捠 側偺偱 暘曣偺傒偵拝栚偡傞丅 捈楍(nr+R) 暲楍(r+nR) 柧傞偝偼 nr+R=r+nR 仺 (n-1)r=(n-1)R 仺 r=R 偺帪摨偠偱 (nr+R)>(r+nR) 偺帪暲楍偑 (nr+R)<(r+nR) 偺帪捈楍偑柧傞偔側傞丅 弌戣幰條 崌偭偰偄傑偡偱偟傚偆偐丅 |
|
(nr+R)>(r+nR) 偺帪偭偰幚嵺偁傞偺丠 |
|
揹抮偺撪晹掞峈偑戝偒偔側偭偰r>R偵側偭偨帪(nr+R)>(r+nR)偑惉棫丅 (nr+R)>(r+nR)偵墬偰 r=kR (k偼揹媴掞峈偵懳偟偰偺揹抮撪晹掞峈攞棪 (k>0))偲抲偔 (nkR+R)>(kR+nR) (nk+1)R>(k+n)R (nk+1)>(k+n) (R>0) nk>k+n-1 (n-1)k>n-1 k>1 (n>=2) 傑偲傔 r<R偺帪捈楍偑柧傞偄 r=R偺帪摨偠 r>R偺帪暲楍偑柧傞偄 |
|
捈楍暲楍偦傟偧傟揹抮懁傪傑偲傔偨忬懺偱丄 晧壸偵懳偟偰棳偣傞揹棳傪x幉 偦偺偲偒偺揹埑傪廲幉偵偡傞偲傢偐傝傗偡偺偱偼側偄偐側丠 偙偺栤偄偼晧壸偑壜曄偩偐傜傔傫偳偆丅 揹棳偐揹埑偳偭偪偐傪屌掕偟偰偟傑偊偽傢偐傝傗偡偄丅 |
|
>r<R偺帪捈楍偑柧傞偄 >r=R偺帪摨偠 >r>R偺帪暲楍偑柧傞偄 偙傟惓夝偱偡丅 揹棳偲揹埑偺傒偱僌儔僼傪彂偔偲丄乽r=R乿偺揰傪偲偍傝傑偡丅 偙傟偼揹抮悢偑n偱傕丄忋婰忦審偼曄傢傜側偄偱偡丅 |
|
慀傞偩偗偺攏幁偼偳偙偵峴偭偨丠 |
|
偙傫側揹抮偭偰扨榋偐丠 |
|
揹媴偺梫媮揹棳偑懡偗傟偽偁傝摼傞 |
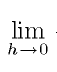
|
h帺懱偼0偱偼側偄偑丄悢幃拞偺1-h傗1/h傒偨偄偵懠偲斾傋傞偐傜憡懳揑偵0偲尒側偝傟傞偩偗 懚嵼偟偰偄傞偙偲偼偄傞偗偳丄堦斒恖偺拞偱偼懚嵼姶偑側偔側偭偰偟傑偆巆擮側壌傜傒偨偄側幰偝 |
|
h偼柍偔側傜側偄 棟惈偱偳傫側偵梷偊崬傫偱傕徚偊偼偟側偄偺偝両 |
|
僼儔儞僗岅偱偼傛偔偁傞偙偲 |
|
0傪亣偵抲偒姺偊傞偲僄僢僠偑偄偭傁偄 |
|
傾僢僔儏偵偼娭傢傝偺偹偊偙偲偱偛偞傫偡 |
|
偲偙傠偱丄偙傟偭偰亣偐傜嬤偯偄偰傞偺丠亅亣偐傜嬤偯偄偰傞偺丠 |
|
偦傟偼偹丄慜偐傜斊偝傟傞偺偲屻傠偐傜斊偝傟傞偺偳偭偪偑岲偒丠偦傟偲傕岎屳偑偄偄丠 偭偰偙偲偩傛 |

|
挊柤側宱嵪妛幰偺懡偔偑 偦偺廂擖偺戝敿傪搳帒偵傛傞棙塿偱偼側偔 島墘椏傗屭栤椏丄挊嶌尃廂擖偑愯傔偰偄傞偄偆帠幚偑 慡偰傪暔岅偭偰偄傞偩傠偆 |
|
>悢妛僩僢僔乕 壗偙傟 |
|
儗僗嘾僋僗 4廳儖乕僾偺4偮栚偺儖乕僾曄悢偵u傪巊偍偆偲偟偨偑 w偵彂偒姺偊偰傗偭偨傢 w偵彂偒姺偊偰傗偭偨傢 娭楢幙栤偱偡偑丄儀僋僩儖傪捈岎嵗昗宯偱昞偟偨偲偒偺屄乆偺嵗昗偺悢抣偼側傫偰屇傇偺偑惓偟偄偺丠 梫慺丠惉暘丠 梫慺偲偄偆偲儀僋僩儖偺廤崌傪峫偊偨偲偒廤崌偺梫慺乮尦乯偲崿摨偟偦偆偱补挪婥偑丄 |
|
偲涤纻獁偩偲廳傒儀僋僩儖偺w偲暣傜傢偟偄傗傫偗 u偵栠偟偨 |
|
偦傟側傝偺恖偑偁傜偨傑偭偰彂偄偨偦傟側傝偺傕偺傪 撉傔偽偄偄傫偠傖傫丅嫵壢彂偲偐昐壢帠揟偲偐庤嬤側傕偺偱傕丅 廍偄怘偄偟傛偆偲偣偢偵丅 |
|
彂偒崬傒傪偟偨恖偵傛偭偰嶍彍偝傟傑偟偨 |
|
娍偼栙偭偰a4(4偼壓晅)偠傖偁両 拪徾嬻娫側傫偩偐傜乽姷椺偱1暥帤乿側傫偰僋僜僋儔僄側傫偠傖偄両 僾儘僌儔儈儞僌偺儖乕僾僇僂儞僞側傜i,j,k,l,乧偲偐a(n)偲偐偄偐偑偱偛偞偄傑偟傚偆偐 >梫慺丠惉暘丠 惉暘偠傖偹丠 |
|
>僾儘僌儔儈儞僌偺儖乕僾僇僂儞僞側傜i,j,k,l,乧偲偐a(n)偲偐偄偐偑偱偛偞偄傑偟傚偆偐 l偼僀僇儞傛l偼僉儈 1傗|偲暣傜傢偟偄傛僉儈 偱偼偳偆偡傞偐丠 偦傕偦傕係廳儖乕僾埲忋偵側傞帪揰偱愝寁傪尒捈偟偨傑傊 |
|
>偦傕偦傕係廳儖乕僾埲忋偵側傞帪揰偱愝寁傪尒捈偟偨傑傊 偟偐偟僗儗暥偼4師尦嬻娫偺榖側傫偩偐傜慡師尦偱 儖乕僾傪傑傢偡側傜嵟掅4廳儖乕僾偵側偭偪傖偆偩傠 張棟撪梕埶懚偱徣偗傞偲偐側傜暿偩偑 |
|
3D僾儘僌儔儈儞僌側傜峴楍偼x,y,z,w偩偗偳丒丒 |
|
>偟偐偟僗儗暥偼4師尦嬻娫偺榖側傫偩偐傜慡師尦偱 >儖乕僾傪傑傢偡側傜嵟掅4廳儖乕僾偵側偭偪傖偆偩傠 僒僽儖乕僥傿乕儞壔傪偟偨傑傊 僒僽儖乕僥傿乕儞壔傪 |
|
>u偵栠偟偨 U偲V偼3D-CG偺僥僋僗僠儍儅僢僺儞僌偺嵗昗偲偟偰堦斒偵巊傢傟偰傞偐傜嬻娫偺嵗昗偵偼巊傢側偄偱偹丅 |

| [0] [1] [2] [3] [4] [5] |