数学@ふたば保管庫 [戻る]
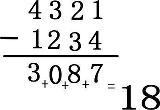
|
2桁で試すと、必ず9になり、6桁で試すと必ず27になる。 |
|
各桁をA,B,C,Dとすると (A-D)+(B-C)+(C-B)+(D-A) このまま計算すると0だけど A,B,C,Dは全て異なるので繰り下がりが必ず2回起こる。 繰り下がると上位桁を-1して下位桁を+10、つまり+9 これが2回なので9*2=18 A<Dの場合は四桁の数字を入れ替えて考えれば符号が変わるだけで同じ。 なんか上手くかけない。 |
|
ほほう なるほど 流石賢いのう |
|
No.90507さんの論理を数式に置き換えてみました。 b-c と c-b の組み合わせについて検証する(但し、b>c) b-c=n とすると、 b-c の1桁目は、b-1-c=n-1 、 c-b の1桁目は、10+c-b=10-n、 右辺同士を足すと、(n-1)+(10-n)=9 a と d の組み合わせについても同様に9が得られる。 以上でOK? |

|
書き込みをした人によって削除されました |
|
>No.90451 No.90452 すごく分かり易くて面白いよ! 分からないのは粘性流体と粘性流体だと高音が減衰しやすい 理由かな。回折の説明がなるほどだった。w 樹状突起と稲妻の形の類似性は本当に偶然なのかなぁ。 分かり易い説明を読んで形を決める要素が違うのは分かったん だけど、自分の出来のイマイチな頭脳には往生際の悪い期待を 鎮めるだけの力が要素の違いだけだと不足みたい。 神経を誘導する化学物質の濃度と稲妻の通り道になるイオンの 濃度、似てる気がする。 頭脳がイマイチなのが申し訳ないよ。 No.90454が理解できたらもっと面白いのになぁ。 面白いレスありがとう。w |
|
>分からないのは粘性流体と粘性流体だと高音が減衰しやすい 粘性流体は文字通り、粘り気のある流体 こういう流体の「一部だけ」を動かそうとすると 粘性で(摩擦が生じ)運動エネルギーの一部が 熱になって散逸してしまうから運動エネルギーが減る 音波は空気の粗密波が進行していく現象だから、 もし粘性が無ければ逆2乗法則で拡散するだけで 運動エネルギー全体は保存するので減衰はしないのだが 粘性があると当然減衰するし、高周波の方が 同じ大きさの音でも「空気の一部分」を動かす回数が 周波数に比例して多くなるので早く減衰する |
|
高周波は速く往復しなきゃいけないので 摩擦で失われるエネルギーが大きくなって 音量の減衰が激しいって感じかな? ゆっくり擦るか速く擦るかどっちが摩擦熱が上がりやすいか ってイメージでいいんかな? |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
>No.90463 今回も解りやすくありがとう。w すごく分かりやすくて面白かった。 >No.90464 イメージがしやすくて面白いね。w 一部だけを動かす時の摩擦が粗密の度合いが大きいほど大きく なるって理解でいいんだよね? 見方を変えたら周波数が高いほど一つの波を発生させるのに よりエネルギーが必要になるとも言えるのかな? 表現が下手だけど、ちょっと分かってきた気がする。 正しい理解になってるといいけどな。 スレを立てた時に比べて随分気持ちがすっきりしてきた。 尊敬できる書き込みを読めてよ嬉しい。 |
|
>見方を変えたら周波数が高いほど一つの波を発生させるのに >よりエネルギーが必要になるとも言えるのかな? 光の話しだけど、 e=hν e:光子のエネルギー h:プランク定数 ν:振動数(周波数) って式があったな 振動数が高いほど光子1個のエネルギーが高い |
|
稲光を担う電荷の正体は何で、 どこから来て、どこへ行くのやろうか… もし電子とかの単一種の電荷なら、電気的斥力でまともな形を保たない希ガス、、 かつ地面から空に立ち上らないとおかしい |
|
ていうか、インターネットに書いてあった、 http://www.saga-ed.jp/kenkyu/kenkyu_chousa/h15/05annzennajikkenkansatu/kaminari040326/400shikumi/frame_shikumi.htm ttp://www.saga-ed.jp/kenkyu/kenkyu_chousa/h15/05annzennajikkenkansatu/kaminari040326/400shikumi/frame_shikumi.htm |

|
lim(n→∞)(1-1/n)^n =lim(n→∞)(1+x/n)^n at x=-1 =e^x at x=-1 (テーラー展開より) =1/e ≒0.36787944117 |
|
スレ主へ そういう変数のベキ乗がある極限は、 対数とってから極限を計算すると簡単ですよ ゆとり教育以前は、高校で必ず習ったやり方だが… |
|
ゆとり以前でも指導要領に入ってないようだが 発展的な内容として教師が教えてくれたとかか |

|
書き込みをした人によって削除されました |
|
メリーくるしみます
かっこいい1ねんせいになるきみへ! 【問】計算複雑性理論(計算量理論)における クラスPとクラスNPが等しくないという予想が 正しいことを証明しなさい。 |
|
何の一年生ですか |

|
>「ぼく」が加わらなければ3人で戦うことになるという前提以外になければその理屈は通る 日本語で書けよ でもNo.90340に反論してると推測して解説はしてやる 競技人口が9人以上なら3人は「ぼく」以外の誰かとチームを組めば良いので「おまえは来るな!」と言える 8人しか居なかったら「ぼく」を入れなければ90%負けるのだから「おまえは来るな!」とは言えない 「おまえは来るな!」と言ってるのだから競技人口は9人以上居る ここまでは判るか? |
|
>日本語で書けよ 日本語勉強しろよw |
|
>日本語勉強しろよw 指摘された間違いというか指摘し様の無い勘違いに それでも優しく窘めてくれた人に逆切れ? さてはオマエ○鮮人だな |
|
>お前バカだろ 同意 よく読めば解ることを 己の拙い理解力を 過信というか盲信する馬鹿が 逆切れとしか言い様の無い 惨めなレスで恥の上塗りをしている |
|
>「ぼく」が加わらなければ3人で戦うことになるという前提以外になければその理屈は通る つまり 「ぼく」が加わらなければ3人で戦うことになるという前提以外に前提がなければその理屈は通る って書きたかったんだろう いずれにしてもその 「ぼく」が加わらなければ3人で戦うことになるという前提 なんて無いけどな |
|
書き込みをした人によって削除されました |
|
50% 自分が参加したチームの勝率の評価 |
|
本来勝率五分五分の人が10戦やったとして、4勝しかできなかったとします。 この1敗分は自分が悪いのか、たまたまへたくそ達と組まされたからか、 どっちですか? |
|
チームの組み合わせも8C4=70有るので、10戦程度では判断が出来無いと思います。 対戦数が増えると勝率は正しい値に近づくでしょう。 |
|
>10戦程度では判断が出来無いと思います。 出来ます 正しい値からは程遠いでしょうが |

|
中学受験で見かけそうな問題よね 円が一つでも増えたら中学・高校レベルになる 製作者のレベルが高いと見るのがスジ 答えは S=36(6-π) πがダメならπ=3.14とでもしときゃええんよw |
|
>S=36(6-π) =36×6-36π =36×12÷2-(6^2)π =直角三角形の面積 - 円面積 |
 こう? |
|
そっから進まないじゃんw |
|
え? |
|
>そっから進まないじゃんw そこまで馬鹿だと清々しいよ |
|
36÷3=12 36×12÷2=216 6×6×3.14=113.04 216-113.04=102.96c㎡ 小6では円周率は3.14と指導しているからね。 |
|
もういろんな人がいろんな答え出してるのに ここにきて得意になって解答w |
|
>小6では円周率は3.14と指導しているからね。 語尾に(ッキリ ってのを足すとオマエの気持ちがより的確に伝わるから次からそうしなさい |
|
>こゆ事でOK? 分かりやすいな 6年と言わずもうちょい下の学年でも解けるのか |
|
余談ですが、 以上の式の「M」を「λ」と書き換えると、ポアソン分布の公式になる事を昨年知りました。(品質管理検定(QC検定)2級の試験勉強をしていた時に気付きました。嬉しかったですね)ポアソン分布を式で表すと、添付画像の様になります。http://www.wolframalpha.com/input/?i=f%28X%29+%3D+%28e%5E%28-%CE%BB%29%29*%28%CE%BB%EF%BC%BEX%29%2FX%21 |
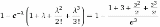 ポアソン分布では、例えば 「ある特殊な血液型を持つ人の確率が1.5%の時、200人中にこの血液型を持つ人が4人以上いる確率を求めよ。λ=3とする(1.5%×200=3)」といった問題の時、添付画像の様になります。http://www.wolframalpha.com/input/?i=1-%28e%5E%28-%CE%BB%29%29*%281%2B%CE%BB%2B%28%28%CE%BB%5E2%29%2F2%21%29%2B%28%28%CE%BB%5E3%29%2F3%21%29%29+%3D+1-%28e%5E%28-3%29%29*%281%2B3%2B%28%283%5E2%29%2F2%21%29%2B%28%283%5E3%29%2F3%21%29%29 |
|
以上より、>>No.90156の近似式は添付画像の様になります。 なお、上式でもそうですがあくまでも近似式なので「=」の部分は「≒」に読み替えて下さい。http://www.wolframalpha.com/input/?i=%28%28V%5EY%29+sum+%28%28W%5En%29%28Y-1%2Bn%29%21%2F%28%28Y-1%29%21n%21%29%29+from+n%3D0+to+%28X-1%29%29+%3D+1-e%5E%28-M%29+sum+%28%28M%5Em%29%2F%28m%21%29+from+m%3D0+to+%28Y-1%29%29 |
|
以前に、>>>>No.90156式の左辺の近似式を求めようとした 事もありましたが、あきらめました。Xやbが圧倒的に大きな右辺と違い、Yやcが非常に小さいためです。(cは1程度、Yは大きくてもせいぜい5以下)仮にX=4とした時、左辺は添付画像の様になりますが、Yが小さいため、W*Yをひとまとめにする事などは出来ませんでした。(Y=5とした場合でも、Y(Y+1)(Y+2)=5*6*7となりさすがにY^3と近似する訳にはいきません)http://www.wolframalpha.com/input/?i=%28V%5EY%29*%281%2BW*Y%2B%28%28W%5E2%29%2F2%21%29*Y%28Y%2B1%29%2B%28%28W%5E3%29%2F3%21%29*Y%28Y%2B1%29%28Y%2B2%29%29 |
|
ただ、面白い事は見つけました。 私が知らなかっただけで、数学の教科書等には載っているかと思います。1+Y+Y(Y+1)/2!+Y(Y+1)(Y+2)/3!=(Y+1)(Y+2)(Y+3)/3!1+Y+Y(Y+1)/2!+Y(Y+1)(Y+2)/3!+Y(Y+1)(Y+2)(Y+3)/4!=(Y+1)(Y+2)(Y+3)(Y+4)/4!などです。http://www.wolframalpha.com/input/?i=1%2BY%2B%281%2F2%21%29Y%28Y%2B1%29%2B%281%2F3%21%29Y%28Y%2B1%29%28Y%2B2%29%2B%281%2F4%21%29Y%28Y%2B1%29%28Y%2B2%29%28Y%2B3%29%3D%281%2F4%21%29%28Y%2B1%29%28Y%2B2%29%28Y%2B3%29%28Y%2B4%29 |
|
以上の、VやWを省いた左辺の式をまとめると、添付画像の様になります。 http://www.wolframalpha.com/input/?i=sum+%28%28Y-1%2Bn%29%21%2F%28%28Y-1%29%21n%21%29%29+from+n%3D0+to+%28X-1%29%29%3D%28Y%2BX-1%29%21%2F%28Y%21%28X-1%29%21%29近似式については以上で終わりです。 |
|
texで書いてくれ |
|
texについて調べ始めましたけど、導入するの難しそう・・・ |

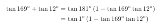 >169+12=181=180+1 どうすんのこれ |
|
3倍角の公式より 3tan3θ=tanθ+tan(θ+60°)+tan(θ+120°) 5倍角の公式より 5tan5θ=tanθ+tan(θ+36°)+tan(θ+72°)+tan(θ+108°)+tan(θ+144°) より Σ[n=0,14]tan(1+12n)° =Σ[n=0,4]{tan(1+12n)°+tan(61+12n)°tan(121+12n)°} =Σ[n=0,4]3tan(3+36n)° =15tan15° =15(2-√3) |
|
15tan15θ°=tanθ°+tan(θ+12°)+tan(θ+24°)+……+(θ+168°) だけでいいだろそれ |
|
加法定理でしこしこ計算し続けるんじゃないのはなんとなく分かる それじゃ難問じゃ無いからな |
|
>15tan15θ°=tanθ°+tan(θ+12°)+tan(θ+24°)+……+(θ+168°) >だけでいいだろそれ 公式:NtanNθ=∑[n=0,N-1]tan(θ+πn/N) の証明は結構難しいよ。 なぜなら、この式が証明できれば、微分することで パーセル問題の解π^2/6=ζ(2)=∑[n=1,∞]1/n^2 が直ちに得られるわけで、少なくともオイラーの 時代には知られていなかった。 |
|
>の証明は結構難しいよ。 初等的には tanθを指数関数表示にすればいいだけなんだが… あるいは母関数使う方法もあるな |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
横やりだが、自分にとって難しいかどうか(知っているかどうか)という部分にだけ反応している子だな。 そのあとの記述の数学史の知識はなさそうだ。今ある知識も先人の努力の賜物なんだろうに。 だいたい、整級数の議論や三角関数のディリクレ核による導入などから三角関数の指数関数表示を現代の視点で理解するのはコーシー等以後だろう。 もちろん発見したオイラーも偉大なのは言うまでもない。 それに加法定理の組み合わせでやってる先の計算もより初等的とある意味言えるが、確かにメンドクサイがそれほど煩雑ではない。 逆に正接の指数関数表示だのベルヌーイ数だのを持ち出す方が説明が面倒だ。 鶴亀算と連立方程式の対比にみられる比喩のようにより一般的で高度なツールを持っていた方が、計算や思考の手間を節約できる場面が存在しうるだろうとか、より多くの問題に対応できる場合があるなど、経験則からくる助言というのならその旨を明示した方が分かりよい。 |

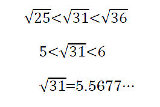
|
x[1]=1とする。 以下の漸化式を数項計算すれば近似値を得る。 x[k+1]=x[k]-(x[k]^2-31)/(2*x[k]) k=1,2,3,4,・・・・ x[10]≒5.567764363 |
|
つ[開平計算] 筆算で平方根を計算できるよ |
|
一般的な問題は、ここで質問するよりも検索したほうが早いよ 開平法 http://www004.upp.so-net.ne.jp/s_honma/root.htm |
|
>No.90169 >No.90179 ありがとうございます コツがわかりました |
|
整数n に対して √n を求めたいなら、 √n = m ± a 、 ただし m は整数で m^2 が n に最も近い値になるもの、 また |a|<1 、と置いて (m ± a)^2 = m^2 ± 2am + a^2 = n これを a について逐次近似で解けばいいよ 2次関数だからNewton法であっさり収束するだろ 実際、電卓もそうしてるはずだし |
| [0] [1] [2] [3] |