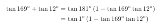
>169+12=181=180+1
どうすんのこれ
数学@ふたば保管庫 [戻る]

|
15*(2-sqrt(3)) |
|
これ解法知って感嘆したやつだ |
|
あからさまな代数的対称性を使って計算できると天才なのか(笑) 私のイメージする「天才」とはかなり違うな |
|
Σ[n=0,14]tan(1+12n)°なのは分かった 後は分からん |
|
169+12=181=180+1 |
|
>あからさまな代数的対称性を使って計算できると天才なのか(笑) >私のイメージする「天才」とはかなり違うな 競技人口が少ないと天才てイメージがわかない有有… |
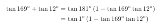 >169+12=181=180+1 どうすんのこれ |
|
3倍角の公式より 3tan3θ=tanθ+tan(θ+60°)+tan(θ+120°) 5倍角の公式より 5tan5θ=tanθ+tan(θ+36°)+tan(θ+72°)+tan(θ+108°)+tan(θ+144°) より Σ[n=0,14]tan(1+12n)° =Σ[n=0,4]{tan(1+12n)°+tan(61+12n)°tan(121+12n)°} =Σ[n=0,4]3tan(3+36n)° =15tan15° =15(2-√3) |
|
15tan15θ°=tanθ°+tan(θ+12°)+tan(θ+24°)+……+(θ+168°) だけでいいだろそれ |
|
加法定理でしこしこ計算し続けるんじゃないのはなんとなく分かる それじゃ難問じゃ無いからな |
|
>15tan15θ°=tanθ°+tan(θ+12°)+tan(θ+24°)+……+(θ+168°) >だけでいいだろそれ 公式:NtanNθ=∑[n=0,N-1]tan(θ+πn/N) の証明は結構難しいよ。 なぜなら、この式が証明できれば、微分することで パーセル問題の解π^2/6=ζ(2)=∑[n=1,∞]1/n^2 が直ちに得られるわけで、少なくともオイラーの 時代には知られていなかった。 |
|
>の証明は結構難しいよ。 初等的には tanθを指数関数表示にすればいいだけなんだが… あるいは母関数使う方法もあるな |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
横やりだが、自分にとって難しいかどうか(知っているかどうか)という部分にだけ反応している子だな。 そのあとの記述の数学史の知識はなさそうだ。今ある知識も先人の努力の賜物なんだろうに。 だいたい、整級数の議論や三角関数のディリクレ核による導入などから三角関数の指数関数表示を現代の視点で理解するのはコーシー等以後だろう。 もちろん発見したオイラーも偉大なのは言うまでもない。 それに加法定理の組み合わせでやってる先の計算もより初等的とある意味言えるが、確かにメンドクサイがそれほど煩雑ではない。 逆に正接の指数関数表示だのベルヌーイ数だのを持ち出す方が説明が面倒だ。 鶴亀算と連立方程式の対比にみられる比喩のようにより一般的で高度なツールを持っていた方が、計算や思考の手間を節約できる場面が存在しうるだろうとか、より多くの問題に対応できる場合があるなど、経験則からくる助言というのならその旨を明示した方が分かりよい。 |