数学@ふたば保管庫 [戻る]
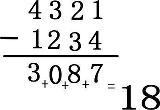
|
2桁で試すと、必ず9になり、6桁で試すと必ず27になる。 |
|
各桁をA,B,C,Dとすると (A-D)+(B-C)+(C-B)+(D-A) このまま計算すると0だけど A,B,C,Dは全て異なるので繰り下がりが必ず2回起こる。 繰り下がると上位桁を-1して下位桁を+10、つまり+9 これが2回なので9*2=18 A<Dの場合は四桁の数字を入れ替えて考えれば符号が変わるだけで同じ。 なんか上手くかけない。 |
|
ほほう なるほど 流石賢いのう |
|
No.90507さんの論理を数式に置き換えてみました。 b-c と c-b の組み合わせについて検証する(但し、b>c) b-c=n とすると、 b-c の1桁目は、b-1-c=n-1 、 c-b の1桁目は、10+c-b=10-n、 右辺同士を足すと、(n-1)+(10-n)=9 a と d の組み合わせについても同様に9が得られる。 以上でOK? |