数学@ふたば保管庫 [戻る]
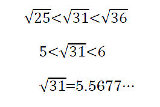
|
x[1]=1とする。 以下の漸化式を数項計算すれば近似値を得る。 x[k+1]=x[k]-(x[k]^2-31)/(2*x[k]) k=1,2,3,4,・・・・ x[10]≒5.567764363 |
|
つ[開平計算] 筆算で平方根を計算できるよ |
|
一般的な問題は、ここで質問するよりも検索したほうが早いよ 開平法 http://www004.upp.so-net.ne.jp/s_honma/root.htm |
|
>No.90169 >No.90179 ありがとうございます コツがわかりました |
|
整数n に対して √n を求めたいなら、 √n = m ± a 、 ただし m は整数で m^2 が n に最も近い値になるもの、 また |a|<1 、と置いて (m ± a)^2 = m^2 ± 2am + a^2 = n これを a について逐次近似で解けばいいよ 2次関数だからNewton法であっさり収束するだろ 実際、電卓もそうしてるはずだし |