∃x P(x) は証明でき - 数学＠ふたば保管庫

数学＠ふたば保管庫 [戻る]

∃x P(x) は証明できるけど
具体的にtを構成して P(t) は証明できないような述語Pってありますか？削除された記事が2件あります.見る

バナッハ＝タルスキーの
パラドックスとか

チャイティンの定数とかはどうかな？
確かに存在しているのに
計算は原理的に不可能っていう

書き込みをした人によって削除されました

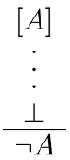
たとえば古典論理で（背理法を使えば）∃x P(x) を証明できるが、
直感主義論理での証明を構成できないケースとかが
当てはまるんｼﾞｬﾈ

具体例は知らん
背理法のシークエント計算をよく見れば何か見出せるかも試練、
見出せたならそれは推論規則を古典論理に固定した下でも背理法で証明するしかない述語ということで、スレの題意を満たす
、希ガス

Rを実数全体の集合とする。
Sを「具体的に構成可能」なRの部分集合の全体とする。
Sの補集合が空でないことを証明可能であるなら、
P(x)を「xはSに含まれない」とすれば良い。
問題は「具体的に構成可能」とは何を意味するのかということだが…。

「具体的に構成可能」が「有限回の手続きで構成可能」を意味するとしたとき、
Sは明らかに可算集合になる。
Rの部分集合の全体は非可算なので、
Sの補集合は空ではない。
ということで、P(x)として「xはSに含まれない」とすれば良い。

変域指定なしで集合定義するとかダメだろそれ

まあPAとか不完全なモデル構成すればよろしい