>��Q�ҍ���
��������
���w���ӂ��Εۊnj� [�߂�]

|
�Ƃ肠������Q�ҍ��� |
|
�v���[���g��0�A1�A2�����Ă���l�̐l����N0,N1,N2�Ƃ���B ��Ԃ�(N0,N1,N2)�ƕ\�L����Ə�����Ԃ�(n,0,0)�Ə�����B N0+N1+N2=n�͖��炩�Ȃ̂�N2���ȗ����� ��Ԃ�(N0,N1)�ƕ\�L����Ə�����Ԃ�(n,0)�Ə�����B ���(a,b)������(a-1,b+1)����я��(a,b-1)�ւ̑J�ڊm���͌v�Z������߂���B ������Ԃ����ԑJ�ڂ�m��J��Ԃ����Ƃ��̍ŏI��Ԃ̕��z�����߂�Ηǂ��B �v�Z���ʓ|�Ȃ̂łƂ肠�����ۗ��B |
|
�������݂������l�ɂ���č폜����܂��� |
 >��Q�ҍ��� �������� |
|
�������݂������l�ɂ���č폜����܂��� |
|
�莮�����͓��v�����I�ȕ��z�ŋ��߂銴���H |
 �Ă��ƁB |
|
N0,N1,N2�̊��Ғl�̑Q�����ɗ��Ƃ��Ȃ��� �����Ă݂���������������B |

|
>�����G�����Ƃ���L�`�K�C No.90044�����悸 �E�u�����v�Ƃ��鍪���Ɣ��f� �E�Ȃ��Ԃ����Ⴏ���u�����Ƃ���v�Ɩ������Ȃ���Ȃ�Ȃ����̍����K���y�ь����N�Q�ł͂Ȃ����Ƃւ̍������� �E�u�L�`�K�C�v�ƌĂт����Ȃ���Ȃ�Ȃ����������Ɣ��f� �����ꂼ�����Ȃ藧����Ȃ肵�Ă݂�����ǂ���H ����Ƃ���ςƉ����Ɋ�Â���my��̉����t���Ԃ�����������������H ��������_�ؕ����F�߂���Ō���Ǝ��ӂ̔O�Ŏ����ӂߎQ�����̂��Ԃ����Ⴏ�ɃV���U�C������ǂ���H ���̂Ƃ����ɂ܂��ė��܂�����Ȃ��̂ɂ��łɃV���Z�C�������Ⴄ�����H ��H |
|
�ȂJ�^�J�i�������Ă邵�A���{������X��a�����郌�X���� ����ɂ��Ȃ������悳�������� |
|
>�����G�����Ƃ���L�`�K�C ���� �ȂL�`�K�C���J�^�J�i������̖��ȓ��{��ŃL�����L�����i���Ă�Ȃ� |
|
No.90057 �����悸 �E�u�����Ȃ��v�Ƃ��鍪���Ɣ��f� �E�Ȃ� No.90057���u�����Ƃ���v�Ƃ������߂ɓ�Ȃ��Ȃ���Ȃ�Ȃ����̍����K���y�ь����N�Q�ł͂Ȃ����Ƃւ̍������� �E�u�L�`�K�C�v�ƌĂт����Ă͂Ȃ�Ȃ������Ɣ��f� �����ꂼ�����Ȃ藧����Ȃ肵�Ă݂�����ǂ���H ����Ƃ���ςƉ����Ɋ�Â���my��̉����t���Ԃ�����������������H ��������_�ؕ����F�߂���Ō���Ǝ��ӂ̔O�Ŏ����ӂߎQ�����̂��Ԃ����Ⴏ�ɃV���U�C������ǂ���H ���̂Ƃ����ɂ܂��ė��܂�����Ȃ��̂ɂ��łɃV���Z�C�������Ⴄ�����H ��H |
|
�ǂ���No.90057 �M�u�� |
|
�摜�̂����Ŋ��S�ɃX������ |
|
�{���ɖ��ʂȉ摜����ȁA�����y������� |
|
���ʂ̏�ɕs�� �s�����Ƃ͂�����ӎu�\������҂������l����̂� �Ȃ�Ŏ~�߂Ȃ��̂��˂� �R����҂��]��ł郄�c����������Ȃ瑼�̔ł����� �Ȃ�Č����Ƃ��̔n�����Εa�� |
|
�W�X��del������ |
|
�������݂������l�ɂ���č폜����܂��� |

|
>No.89627 �Ȃ�قǁA�u����������ق���葽�������������āw�P�{�x�v���B �����Ɓu�f�t�H���g�́w�Q�{�x�𗪂��āw�{�x�ƕ\���v���Ǝv���Ă��B |
|
�������ォ��{�͂Q�{�̂��Ƃ��������A���m�����i��Ŕ{���̈Ӗ��ɂȂ������߁A�������������B��������ׂ������W�N�ɐ��{���o�������[�� �u�������������e�v�Z���{�m�ď̃��~���A�]�O�m���K�����j��{�g�L�V���n��{�g��������A���|�z���A栃o������~�m��{�n��~�A�\�{�n�\�~�g�v�Z��V�g�S���v �v��F�����ɂ��鐔���̌v�Z�������ł́u��{�v�̌Ăѕ��i�Q�{�̈Ӗ��j���~�߁A���܂ł̈�{�Ƃ���Ƃ���͓�{�̈Ӗ��Ƃ���B |
|
>�������ォ��`�����W�N�ɐ��{���o�������[�� ����Ȃ̂͂�����̃��X�ɏo�Ă� ���u�������͕̂�������̓�{�͍��̉��{�����Ď��� |
|
���O�͌����\�̓[�����o�J���ǂ����ŌĂꂽ���� http://ja.wikipedia.org/wiki/%E5%80%8D |
|
��Ƃ����邩�爫���� �l�̔{�����ł��� |
|
>���O�͌����\�̓[�����o�J���ǂ����ŌĂꂽ���� �������Ȃ��n�����ċt�ꂵ�Ă����������X�������� |
|
>�������Ȃ��n�����ċt�ꂵ�Ă����������X�������� �o�J���m���ǂ���������̂ɂ� |
|
>�o�J���m���ǂ���������̂ɂ� ���Ⴀ�u���F�B�ɂȂ��Ă��������v���Č��� |
 �{������ |
|
>>���O�͌����\�̓[�����o�J���ǂ����ŌĂꂽ���� ���w�ŃE�B�L�������ɂ���z���Ă܂������ ������ |

|
>���w�I�Șb�͂Ƃ������A�_���I�Ȗ��Ƃ��āA ���R�������ėv��Ȃ����� >7��̑ΐ��S�ăp�[�ŏ��� �͕̂s�\�ł͂Ȃ��B �O���łȂ����P�O�O���ł͂Ȃ��B ���炽�珑���Ă邪���e�͂��ꂾ���� |
|
>�Ƃ����}���͕K���������藧���Ȃ��A�Ƃ����̂𗝉����Ă����˂Ȃ�Ȃ��Ƃ������Ƃ��� ����͑S������Ȃ��� �u�Ƃ͂Ȃ�Ȃ��v�ōςޘb���� >���w�I�Șb�͂Ƃ������A�_���I�Ȗ��Ƃ��āA ���ꂾ���ĉ����Ƃ������Ȃ̂������ς肾�� �������Ă݂�Ɗm���Ƀ��_�������� �Ƃ������قƂ�ǂ����_���� |
|
>���w�I�Șb�͂Ƃ������A�_���I�Ȗ��Ƃ��āA �ʔ����Ȃ� �����݂ǂ��떞�ڂ����� |
|
���x�ȐS���킾�� �p�[�A�p�[�Ƃ��Ď��͂������Ƀp�[�ȊO���낤�Ǝv�킹�Ƃ��� �܂����̃p�[�A�� |
|
�������݂������l�ɂ���č폜����܂��� |
|
>���x�ȐS���킾�� ����������A���p�[�ŗ��鑊��Ɉ��ڂ̓p�[���o�� �A���p�[�Ȃ�p�[�ő��q�ɂȂ� �A���p�[�ɏ��ׂɉ����`���L���o���Ɨ\�z���đ��肪�O�[�ŏ����ɗ����珟�Ă� �A���p�[��f���胂�K�ŗ����Ă��ꂪ�`���L�������ꍇ�Ɖ��̑��q����\�z���ď��Ă�`���L���o���ꂽ����߂� ���������ڂq�ɂ�����S�����ʂ͔��Q�� �ȏ����̋�_�ł��� |
|
����̃N���u�ɘA��폟�̃}�}������ �A��A���Ƃ͖����Ȃ��̂��S�肾�Ƃ� �������}�}�̃^�C�~���O�ƃe���|�ŏ������Ȃ��Ƒʖ� �����ɏ폟�̔閧������炵�� |
 �{������ |
|
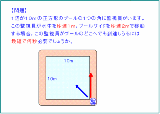
���c�E����v�q�l�̖��ȁu�`���L�̐_���܁v���܂��傤�B |
|
�{�C�Ō��Ă���l�������p�[�Ȃ̂ł��B |
|
�Ώ̐����Ίp���� �X�l���̖@�� �P���ɍs�����@�Ɖ�肱�ޕ��@��2�̎��𗧎� ��_�ƂȂ�Ƃ������� |
|
�v�[���ɐ��������Ă���Ƃ͂ǂ��ɂ�������Ă��Ȃ� |
|
>�v�[���ɐ��������Ă���Ƃ͂ǂ��ɂ�������Ă��Ȃ� �������ˁB���ꂾ�ƃv�[���T�C�h�ȊO�̕����͈ړ����x������Ȃ�������Ȃ��ɂȂ�� |
|
�������Ă�q���g���Ė��f�]�ڂȋC�����邯�Nj��͂Ƃ����́H |
|
��@�ɓ���������Ă�����Ȃ́H |
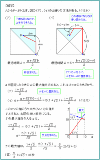 ���� |
|
�������ԉ����̖��H |
|
�X�l���̖@���ʼn����ɂ͂ǂ��������H |
|
>�������ԉ����̖��H 150����2�� 1��ɂ�75��������75�� |
|
>�������ԉ����̖��H 150����2�₾���� 1��ɂ�75�� |

|
�q�|�N���e�X�̎O�����c�B ���w�Z�A�������T�N���ł����e����Ȃ��ȁB ���Ȃ�Ƃ������B |
|
�q�|�N���e�X�̎O�������O��Ȃ�����邯�� �ȂL���C�ȉ~����Ȃ��̂�������Ȃ��Ǝv���Ă��B |
|
���w���̒m���ʼn����邾��H ���w�����Ɣ��~�̖ʐϏK��Ȃ������H |
|
>���w���̒m���ʼn����邾��H �Ԃ̎ΐ��ŋ��ꂽ�O�����ӂ��̍��v�܂ł͌v�Z�ł���� |
|
�������Ucm^2�ɂȂ��� |
|
�y�����z �U���u �y���z �S���Q�~�S���Q�~�R�D�P�S�{�R���Q�~�R���Q�~�R�D�P�S�|�T���Q�~�T���Q�~�R�D�P�S�{�R�~�S���Q���U >���w�Z�A�������T�N���ł����e����Ȃ��ȁB >���Ȃ�Ƃ������B ���w�T�N���ł��[���ɗ����ł��܂� |
|
���߂�A���t���炸�������B ���s�̎w���v�̂ł͉~�̖ʐς͏��U�̓��e�ŁA �J�c�I�͏��T�̂͂�������A�����鎞��������Ȃ��A �Ƃ������肾�����B �Ⴆ�Ώm�ŋ����Ďq�ǂ��������ł���A�Ƃ����̂͏\��������B |
|
>���߂�A���t���炸�������B ���߂�A�����炱�������m��Ȃ����� �~�̖ʐς͂U�N�ŏK���� ����ɍ��w�N�Ƃ�����邢�g�ōl���Ă� |

|
p=10�̗�ł����� c��1���₷��20-10�~(9�̏o����)���������� |
|
S(n)=��[k=1,n]k=n(n+1)/2 S(n,p)=S(n)%p �Ƃ���B f(p,0)=��[n=1,2p]S(n,p)�ł��� f(p,c)=f(p,c-1)+p(2-[S(n,p)�̂���p-c�̏o����]) �Ȃ̂ł܂���S(n,p)�̏o�����z�ׂ����B p����f���̏ꍇ,0<=n<m<p�Ƃ���� S(m,p)=S(n,p)��n(n+1)/2=m(m+1)/2 mod p ��m(m+1)-n(n+1)��2p�Ŋ����� ��m^2-n^2+m-n = (m+n+1)(m-n) ��2p�Ŋ����� ��m+n+1=p �Ƃ����Ƃ���܂ōl���܂��������M�͂Ȃ��ł��B |

|
���ʎ����������ł���O���̐��̂������ 121 143 165 169 187 231 253 273 275 297 299 341 363 385 441 451 473 483 495 561 583 651 671 693 781 861 891 961 �����̓`�F�b�N����Ƃ킩�邪�S�č����� �^�����Ȃ����͂܂�Ȃ��̂� �����ė͋Z |
|
���P0�O�Q�{���P�O�{���������炁���O�Q�{�����{�����O �������Č����� |
|
2ch���̂܂܃R�s�y���� |
|
�����͂������̂ق����������� |

|
>�N�̕��������I�ňЈ��I�Œ����I�ɓǂ߂�B �����I�ňЈ��I�Œ����I�ɓǂ߂�̂͌N�̂��̔ڋ��Ȑ��i�Ɉ�����̂� |
|
>�܂Ƃ��Ȑl��ID�������Ă�����Ȃ��� >���낻�등���� ID�������牽���ς��́H ��������͂������Ȃ�ق��Ă����������Ȃ� ������čr�炷���c�ɍ\�����c�͍r�炵������ �����Ȃ���r�炷���c�ɍ\���l���ۂ��ĂȂC�� |
|
>�܂Ƃ��Ȑl��ID�������Ă�����Ȃ��� ���Ȍ����~�̋����r�炵��ID�������č��鎖�͂Ȃ� ���̂܂Ƃ��Ȑl�Ƌ�ʂ���̂��Ӗ����킩��Ȃ� >���낻�등���� ��������͂�����Ȃ炳�����Ƃ���� �����Č��ʂ��o�� �b�͂��ꂩ�炾 |
|
�X���b�h�𗧂Ă��l�ɂ���č폜����܂��� |
|
100���{�ɂ��Đ����ɑł��Ԃ����I ���̒n�\���Ԃ�����������O�̊��_���Ă������q�̏o�������I�I |
|
>���̒n�\���Ԃ�����������O�̊��_���Ă������q�̏o�������I�I ���܂��͈�x�����I�I |
|
>�܂Ƃ��Ȑl��ID�������Ă�����Ȃ��� ���̘_���͍��܂łɊ��x�ƂȂ��J��Ԃ���Ă��� ���_�͂����� �����Ă�����Ȃ��������Ă�����Ȃ� ����͂܂Ƃ��Ȑl���r�炵�Ă�l�� ID�����ʂ�����͎̂����A������r�炵�ɑ��Ă� ���̐��w�̍r�炵�͎��Ȍ����~�^�̍r�炵��������ʂ͖��� |
|
�����������Ă���̂�������Ȃ� �����ēV�˂Ǝv���ď�������ł�́H |
|
�X���b�h�𗧂Ă��l�ɂ���č폜����܂��� |
|
>>�����Ȃ����� �������w�ł��� �m���_�̌v�Z�ł��� �������Ă�̂ł���߂̓��������̂��������� |

|
�������݂������l�ɂ���č폜����܂��� |
|
>100�l�̍��v�l��16345.0�`16354.9cm�̂����ꂩ�ŗL���� >�K��16350cm�Ƃ͌���Ȃ��B �i���̋��l���H���[�� |
|
>�i���̋��l���H���[�� 100�l���̍��v�l |
|
�������݂������l�ɂ���č폜����܂��� |
|
�������݂������l�ɂ���č폜����܂��� |
|
�������݂������l�ɂ���č폜����܂��� |
|
100�l�̕��ϒl��163.5cm�ƌ������� 100�l���̐��l��[���Z]�������Ԍ��ʂ̒l��0.1cm�P�ʂ̐��l�ƂȂ�B ��Ƃ��� 163.5cm��99�l�A163.0cm��1�l�̏ꍇ ���v�����16349.5cm�ƂȂ�B���ϒl��163.5cm�ƂȂ�B |
|
��ׂ鎖�ŕs���N���K�i�O���ǂ��l�Ԃ������l�Ԃ��ƃ��b�g���͂鎖�ƍs�����鎖�ɈӖ��͂Ȃ� |
|
3)��1cm�̒��w��99�l��16350-99cm�̒��w��1�l�̎��������Ȃ��B ����Ȓ��w�Z�͌��Ă݂����� |
|
���A130cm�ȏ��10cm��肩 �����悤�Ȃ̂Ŕ���ł��������� |
| [0] [1] [2] [3] [4] |