
本文無し
数学@ふたば保管庫 [戻る]

|
>No.100732 よほど悔しかったんだな そしてその悔しさを紛らわす術の無い自分にイラだったんだろうな まず自分に効果があった煽りを相手にも同様の効果があると思いこみオウム返し 間髪入れず他のレスもオウム返し 連投でオウム返し反論なんてよほどのバカじゃなきゃやらないよな |
|
書き込みをした人によって削除されました |
|
>「「展開図であること」と「辺 ab は 4cm であることが題意であること」とが本当に命題的同値だとでも?」 同値ではないし誰も同値を匂わすようなレスはしていない 幻覚が見えるなら医者に行け |
|
余った部分はのりしろだろ。 |
|
のり代はハサミで切った |
|
う〜ん、「六面体」かなあ? 図上で6cmと書かれた辺とパッと見で合わない長さの辺を 「合う設定で考えろ」ってのがこのテキトーな作図のお告げだと解釈すると、 パッと見で直角のとこも疑わないといかんからなあ あー、超テキトーな教師の弁護せんならんのは鬱陶しいわ |
|
仕事であからさまに組み合わせないもの送ってきたら始末書だよ >ぶっちゃけ私見なのですが、そもそも辺 ab は 4cm であることが「本当に」題意なのかどうか疑問なのですよ。 図を見れば分かるけど上の6cmと横の辺はどう見ても同じ長さじゃない |
|
立体の名前という問題なのだから四面体でも直方体でも問題ないのでは? ともに立体の名称という条件を満たしているのだから |
|
これはわざと見た目の長さを異なるものにして惑わせる問題だろうね多分 やけにケンカ腰な子がいるがそんな言い合う内容かこれ? |
|
はさみ許可ですか この設問 |
|
https://ja.m.wikipedia.org/wiki/ねじれの位置 直線のねじれというのもあるし |

|
>どの理由でdelしたらいいですか? え?荒らし・嫌がらせ・混乱の元で君をdelすれば良いじゃん |
|
指数と密接だからセットで概念を叩き込め |
|
logを最初に習った時、こんなん何の役に立つんだろうって不思議だったなぁ |
 本文無し |
 本文無し |
 本文無し |
|
熱力学やったら家計簿を Exp進法でつけたくなりました |
 >log苦手 ぶっちゃけ計算にlnばかり用いると、確かにlogが苦手になる気がするのですよ…。事実、logは結構不便なのですよ…。 |
|
あいかわらずキショい画像で荒らしてるけど 数学やってるかたわものはこういう絵が好き だから delしないんだよな おーキショい |
 ログ |
|
>No.100651 ぶっちゃけ、スレ題意は3次元空間だったのですよ。 忘れていただけたら幸甚なのですよ…。 |
|
ぶっちゃけ傾ける方向が90度ちがっていますよ x=x y=x^2 z=z としてパラメーターが(x,z)の2個有る平面として考えればいいのでは |
|
>ぶっちゃけ傾ける方向が90度ちがっていますよ 一般にx-y平面上での45度回転は左回転(θに45°を加える)なので、 y=x^2のグラフの45度回転はぶっちゃけ氏のplotでOKでは? |
|
xy平面に対しって言っているからxy平面の中にある何かの線回りの回転と考えた方がいいのではないかとおもうけど。 数学的表現ではないけど。 |
|
3 次元空間で放物線(t,t^2,0)をx軸回りに45度回転させるとどんな式になるかとかいう(t, (√2)*t^2,-(√2)*t^2)的な媒介変数を使って書くといい話かも |
|
ぶっちゃけ氏 生きてたーー |
|
お久しぶりです エロゲとテンソルにこってます |
|
書き込みをした人によって削除されました |
|
>3 次元空間で放物線 >y = x^2 >をxy平面に対し 45 度回転させたときの放物線の式はどのようにして求めたらよいですか? y = x^2 のグラフ自体はxy平面に埋め込まれてるよね。 もし「xy平面に対し xy平面上で 45 度回転」させるのであればxy平面上で完結した話なんだから 何も3次元空間に設定する必要ないのでは? そうではなく「xz平面方向へ 45 度傾けるように回転」させたかったり 「xy平面に対し z軸方向へ 45 度回転」させたいのであれば なぜそのように書かないの? 回転方向がill-definedでは? |
|
固いこといわず答えよろしく |
|
体構造と全順序が両立しない、というだけで 特に不具合はないのでは? 例えば実数体について、10は他のどの実数よりも小さい数とし、 10以外の実数どうしを比較した場合は通常の順序であるような、 全順序を定義したとすると、 a=8,b=9,c=1のときは(1)が成立しない、 a=2,b=5のときは(2)が成立しない、けど、 体構造と全順序の定義としては、特に不具合ないと思ゆ。。。 |
|
なるほど分かりました。 ありがとうございます。 両立するというのは順序の付け方を(一通りに?)限定するということですね。 |
|
(1)と(2)から (2') a≦0 かつ b≦0 ⇒ ab≧0 は示せる? |
|
(1)より a≦0 ⇒ a+(-a)≦0+(-a) ⇒ 0≦-a 同様に b≦0 ⇒ 0≦-b (2)より -a≧0 かつ -b≧0 ⇒ (-a)(-b)≧0 ⇒ ab≧0 こうでしょうか。 体の性質は証明せずに使いました。 |
|
おそらくそれで合っていると思われ。 ところで実数体について、体構造と両立する全順序は一意に決まる(通常の順序関係のみ)のだろうか。 あるいは通常とは異なる順序関係が存在するのだろうか。 暫く考えたけど分からずじまい、、、 |

うーん、これも違う
 ちょっとは良くなってるんだが・・・ |
もうちょい
 オプティマルfまでもう少しだ。やっぱ100万から億までは10年以上はかかる |
10年で100万が8400万か
 うん、悪くないね |
|
√3だけ二乗みたいな操作を許すなら 問題になる部分だけその数で割ればええんちゃう? |
|
とゆか代数方程式の解であるならその方程式に代入すれば0になるよね |
|
x=(10-4)/(5-3)=6/2=3とか x=log2(8)=log2(2^3)=3とかならわかる。 でも√3を2乗して3にするって意味わからん x=√3=(√3)^2=3って言いたいの? |
|
>実数解に加減乗除を施すことによって最終的には必ず整数にできると思うのですが、 そもそも前提が間違っているぞ スレ主は「実整数が係数の代数方程式」しか頭に無いようだね(笑) 一般的な代数方程式は、複素数体上のものなので 実数解が「代数方程式の係数を加減乗除や累乗根で変形したもの」 であっても、それを「整数にできる」という保証は全く無い |
|
x^5+2x^2+3x+7=0 の解aは a(a(a^3+2)+3)=-7を満たす、とかいう話? |
|
ガロア理論とかそんな話? |
|
クロネッカーを読まれたら |


ユロドル単体バックテスト結果1
 現在実運用しているパラメーターの方です。 酷い結果だ |
ユロドル単体でのバックテスト結果2
 パラメーターがちょっと違う 同じシステムでもそれだけでかなり結果は異なる |
|
4万円あったら…゜。+゜(*′▽`*)。+゜。゜ |
ユロドル単体のドローダウン処理修正結果
 ほとんどかわらねえ・・・ |
ユーロドルはおかしい
 フィルターをかけると普通は良くなるはずなんだが逆に悪くなるのがユロドル |
更にフィルターをかけてみる
 ちょっとはマシになったか |
|
いいから1年周期のsinを入れて20年儲かるかどうかやってみろ |

なんじゃこりゃw
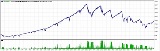 がっかりな資金曲線 しかし実戦で痛い目に合うまでに気付いて良かった現時点ではまだ数学的に適切な投資比率にはなっていないし、パラメーターも改善の余地があるのでそれを修正後に適切な投資比率を算出することで更に改善できる |
こっちも変わらん・・・
 ポンド円の資金率を20%から15%に縮小した上で、ドローダウンの処理を変えてみたけど全く結果は同じだった・・・ 資金率が減っている分だけ利益も減っただけだった |
ポンド円トレードルールのパラメータを変更
 あーら不思議 投資比率15%なのに20%の時の利益を越えてしまいました |
更にパラメータを変更
 まあこんなもんだな、あまりフィルターをかけすぎると逆にエッジのある取引にまでフィルターがかかってしまい効率が悪くなる |
| [0] [1] [2] [3] |