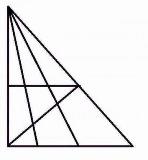
25は左上の黒い三角形です。
数学@ふたば保管庫 [戻る]
|
テスト |

|
数学はナイフ 数学者は、ナイフそのものを、作ったり、切れ味をみる。 物理屋は、ナイフで、物を切ったり、削ったりしてる。 化学屋は、ナイフで切ろうとしてるが、いまいち。 生物屋は、ナイフがさやの中に・・ |
|
経済屋はナイフを大剣と言い張って使いこなしてる振りをする。 |
|
化学屋や生物屋はナイフ使えるようにするためにまず分厚い殻をハンマーでわらなあかんねん 経済屋はナイフを実演販売 |

|
話がすごい方向に |
|
>次に『等しい確率』は断定表現なのでおかしい >『同様に確からしい』が正しい >ただしこの文章においては『同数』で充分 わかったのかい?お馬鹿さん |
|
>ただしこの文章においては そうだな この設問においては、正しいな 普通、買うって言ったら買った傍から補充するとは考えないからな |
|
>この設問においては、正しいな この設問においては、な No.96626は広義においての意味に拘る頭の固い子なんだろうな |
|
自演でした |
|
>自演でした やっと認めたか もう二度とするんじゃないぞNo.96810 |
|
早く子のスレが消えてくれと手を摺り合わせて嘆くNo.96810 |
|
そうそう バカな奴は書き込みしないで欲しいよな 自分を省みない奴とか |
|
>No.96626は広義においての意味に拘る頭の固い子なんだろうな それにしてもしつすぎる 病気だな 生まれはどこなんだろうな |
|
>早く子のスレが消えてくれと手を摺り合わせて嘆くNo.96810 蠅はNo.96626とNo.96628だなw |
|
25は何なんだ? |
 25は左上の黒い三角形です。 |
|
25がありなら30までいけるやろ |
|
25はひどいな |
|
25がありなら線上は全て微小な三角形の集合ですって言い切れてしまうではないか |
 本文無し |
|
【問題】この中に三角形はいくつあるでしょう(25個以上でGoogle社員の素質あり) ってやつだけど、ソースが見つからない。どうやらネタらしい。 |
|
歌えば分かるのに |
|
エビエビシシービ シビエデビ! エビエビシシービ シビエデビ! ......歌っても分からん! |
|
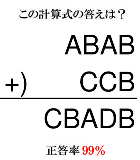
ABBA+CCB=? |
|
なるほど A=ガ B=ン C=ギ D=? ということか。2レス目の意味がようやくわかった |
|
この計算式の答えはCBADBだぜ おまいら設問がわかってない |
|
書き込みをした人によって削除されました |
|
ガンガン ギギン |
|
おまいら=正答率残りの1% |
|
けっこうしつこいねミキ |
|
書き込みをした人によって削除されました |

|
×スペリングと同音異義語の話を無意味に混同するのも「ことば」を覚え始める年頃なのかな? 〇スペリングと同音異義語の話を無意味に混同するのは「ことば」を覚え始める年頃だからかな? 馬鹿垂れ流しw |
|
>おれは区別つくよ ふーん じゃあ「はし」 これは? 区別つくんだろ? オ マ エ は ♡ |
|
>BLACKは英語ですがブラックは日本語で〜っす これも字なら判別できるが音読しても判別つくのか? No.96527は独り善がりでは? |
|
>馬鹿垂れ流しw 単文で自動翻訳通してるの? 解説してあげると、「するのも」は「日本語覚えたて」に係っているんだよ 係助詞ってやつね >区別つくんだろ? 問いが変わったんだから答えも変わるわな No.96525 の例文で「はし」の区別がつかないのは残念な脳なんだね それと最後の一文読もうね♡ >No.96527は独り善がりでは? No.96523ではスペリングにおける不可逆性(L or R →まとめてラ行)を 書いたつもりだったんだけどな 単語として「black」の音読で言えばlaは日本語の「ラ」に近いから単音では判別難しいけど 英語は末尾の母音を発音しないので区別できるよ |
|
>解説してあげると、「するのも」は「日本語覚えたて」に係っているんだよ 突っ込まれてるのはソコじゃないと思う × AするのもBなのかな? △ AするのはBだからかな? 俺的には更に 〇 AしちゃうのはBだからかな? 馬解説が頓珍漢って馬鹿の上塗りだな |
|
>BLACKは英語ですがブラックは日本語で〜っす 「和製英語」とか「英語の片仮名表記」とか日本語か否かの判断は簡単じゃないよね そもそも日本語って何ぞやって問題もあるし 発音で区別できるから判るってのは勝手な個人の考えに過ぎないね |
|
ジョークは日本語です! 日本語なんです! |
|
>突っ込まれてるのはソコじゃないと思う 同じ意見だ 算数馬鹿には分かるまいが |
|
数学の話題と関係ないどうでもいい話題だとみんな途端に元気良くなるな |
|
文句ばっかりだね君は |

|
今から行けば? 通信制とか |
|
>No.96457 階乗数の逆数の総和ってπじゃなくて ネピア定数のeじゃね? |
|
>No.96457 πが出てくるのってバーゼル問題じゃね? 平方数の逆数の話=(π^2)/6に収束 |
|
>まったく無関係のπになるの? 無関係じゃないよ 幾何学的に考えると、あれ「円周の長さ」を級数和で 順番に近似していってるのと同じだからね |
|
>No.96457 階乗数の逆数の総和が、なぜ自然対数eになるのかどなたか解説してくださ... - Yahoo!知恵袋 http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1393202648 |
|
ありがとうございます 通信制大学も資料請求してみました 勉強したい |
|
有理数の和がなして無理数(超越数)になるんか知りたかった みなさんありがとう |
|
無限個足すからだろ √2=1.4142...=1+4/10+1/100+4/1000+2/10000+... |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |

|
方べきの定理による解法発見 因数分解で 積=積 にしてた なるほど |
|
a<bとして 半径bの円Oを書いて半径をOPとする。 OP上にOQ=aとなる点Qをとり、Qを通るOPの垂線を引く。 その垂線と円の交点の好きな方をRとすればQRが求める正方形の一辺。 ∵方べき 一頂点を共有してる理由が分からん |
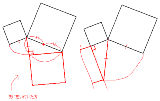 このような配置を連想させるヒントではないかと |
|
【高校受験2015】千葉県公立前期<数学>講評…時間配分がポイント 2015年2月13日(金) 12時22分 http://resemom.jp/article/2015/02/13/22885.html > (5)の作図は、三平方の定理の応用や、円を利用して直角をつくることが求められるなど、受験生にとっては解法に気づきにくいものだったと考えられます。 「円を利用して直角をつくる」ということは、やっぱり円周角の発想につかまった感じかな。 |
|
2015首都圏公立高校入試 > 千葉 > 数学(前期) http://www.tokyo-np.co.jp/k-shiken/15/cba/cba1/cba-su/su-a_1.html ここでも半円弧に対する円周角で直角を作ってるな…… 何か自分の方に見落としがあるような気がしてきた…… |
|
あれ?「半円弧」?「半円周」? 辞書にあるのは「半円周」だな。。 |
|
1 |
|
1次元の場合から数えてみれば |
|
分離って一つずつにするのか? nに依らず1通りだろ |
|
ごめん >n-1次元平面 こうだった |
|
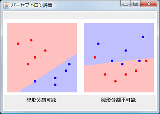
d次元空間の一般位置にある(←重要)d+1個以下の点は d次元空間における超平面(それ自体はd-1次元)で 任意の組み合わせでの分離でいける (例:平面上の一般位置にある3点は直線の引き方次第でどうとでも分離でいける スレ問はn次元空間に対してn点なので、全部一般位置なら Σ[i=0..n]n_C_i通りの分離がでいける (平面に対する符号の違いも区別 |
|
↑間違ってるよ 簡単にして2次元平面で考えてみたらどう? |
|
勘違いすまん n次元にn個の点か |
|
>点の集合{(d1,...,dn)|di∈{-1,1},i∈{1,...,n}} 2^n個の点だよね? |
|
では次にリーマン幾何空間で考えてみよう |
|
del |
| [0] [1] [2] [3] [4] |