数学@ふたば保管庫 [戻る]
|
>部分集合に最小限が必要なんだっけ 最小元な つまり半無限区間(を含む部分集合)だと順序化できないと言いたいようだが 任意の実数の部分集合は 必ず有限長の閉区間の線分(たとえば[0,1])に1対1で射影できるんで 射影してから普通の不等式で順序化すれば何の問題も無いよね |
|
開区間と閉区間は同相ではないけど全単射はつくれるのか なるへそなるへそ |
|
>任意の実数の部分集合は >必ず有限長の閉区間の線分(たとえば[0,1])に1対1で射影できるんで それ、具体的にはどうやるんだ? (−∞、∞)→[0,1] の写像を具体的に示してくれないか? |
|
1/2 + (tan^(-1)x)/pi |
|
それ開区間じゃない |
|
>必ず有限長の閉区間の線分(たとえば[0,1])に1対1で射影できるんで >射影してから普通の不等式で順序化すれば何の問題も無いよね それだとさ Rの任意の部分集合A_λに対して[0,1]への射影f_λが存在して、f_λを使って定義されるA_λの順序関係≧_λがあるわけだよね それって整列順序の定義として問題ないのかな つまりA_λは順序関係≧_λのもとでは確かに最小元が存在するけど部分集合ごとに全然違う順序関係を使っていいのものなのかな |
|
射影しつつ無限遠点を加えてコンパクト化するのは 「無限」の扱い方では割と常識だと思うのだが |
|
>射影しつつ無限遠点を加えてコンパクト化するのは >「無限」の扱い方では割と常識だと思うのだが それは確かに誰でも知ってる常識だが、この話と関係するのか? |
|
Wikipedia(整列集合)より >選択公理を含む集合論の ZFC 公理系からは、実数全体の成す集合 R 上の整列順序が存在することが示せる。しかし、ZFC や、一般連続体仮説を加えた体系 ZFC+GCH においては、R 上の整列順序を定義する論理式は存在しない[1] フェファーマンの結果とのこと |
|
つまり、 「R上の整列順序は確かに存在するが それを具体的に表現することは不可能である」 ということ? |



|
http://hayabusa6.2ch.net/test/read.cgi/loto/1430317616/412 |


|
わかりま線形代数 |
 物理版 |
|
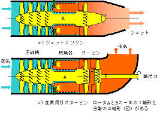
軸が回転してない状態で、燃焼室に直接送風機で圧力かけたとしても 運転時と同様の風の流れになるぞ 始動時の方向を維持するわけじゃない |
 ついでで、ジェットエンジンの風物詩 ショックダイアモンドの解説があったわ |
|
スレ主の高校卒的な静水力学の思考方法では解けないよ 揚力や霧吹きの原理を理解しましょう、そうすれば、なんとなく脳内シミュレーションできる 数学的には、動水力学と圧縮流体をぐぐれ |
|
でた。 適当にそれっぽい言葉を並べて説明しない奴 |
|
>No.96658 説明出来ない時点でオマエはスレ主以下で数学板には要らない子 |
|
流体は流れにくい方向より流れやすい方向に流れようとする性質があります。 ですのでジェットエンジンを設計する際は、吸気口側より排気口側の方に流れやすいように設計します。 スレ画で言うなら始動時に左から右へと流れが出来ており、 すでに流体が左に流れにくい状態になっています。 さらにジェットエンジンの設計が左から右へと流れやすい構造になっているため 燃焼により発生した圧力による流れも左から右へと流れます。 バルブレスパルスジェットエンジンでググルと原理がよく解るかもしれません。 流体の性質を数学的に証明、説明しろというのはさすがに難しいですが。 |
|
理解できても解説が出来ない人や解説できても理解してもらえない人は安易にレスしないでください ぐぐれと命令されると不愉快ですよ |
|
>流体は流れにくい方向より流れやすい方向に流れようとする性質があります。 >ですのでジェットエンジンを設計する際は、吸気口側より排気口側の方に流れやすいように設計します。 ここまでは、問題文を言い換えただけ 以降は、これを根拠として説明したつもりになってるだけ |
|
ターボファンエンジンの動作モデル つべにもあるけど解説米つきなんでニコから http://www.nicovideo.jp/watch/sm23231291 |
|
レベル低い |
|
車のナンバーは4桁目に0が使われてるけど、それを排除する理由は? |
|
9*9*8*7=4536 |
|
4桁目は空欄で0表示は無いでしょ、4桁ナンバーが好きなんだ 4536通りかぁ意外と多いな ありがとうです |
|
豆知識
自動車のナンバーは、下2桁の42(死に)と49(死苦、轢く)が欠番。 ただし希望番号の場合はこれらのナンバーも出してくれる。 |
|
希望ナンバーの抽選番号と人気ランキング http://usedtrucks.blog.fc2.com/blog-entry-375.html 抽選対象番号は地域によって違うって知らなかったよー |

|
割合は想像に依存する |

|
表面積 裏面積 合わせて両面積 |
|
いつでもどんなときでも微分積分だよ |
|
間違えた 俺が信じられないのは 球の表面積が 4πr^2 ってこと これによく気が付いたと感心した |
|
まず円柱から円錐をくりぬいた図形から球の体積Vを求める 次に球面を細かく三角分割しそれらを底面に持ち頂点が球の中心と一致する三角錐に球を分割する 球の体積Vを三角錐の体積の総和として表すとV=Sr/3となって体積から表面積が求まる 微積分のありがたみを感じる |
 微積分さんまじかっけえ |
|
区分求積すればすぐに出るよ |
|
学校教育も公式だけじゃなくて そこに至った経緯とか あるいはなぜそうなのかという詳しい解説も教えるべきなんだろうけど 前に話題になった小学生なら教わらなくてもわかっちゃうんだろうな |
| [0] [1] [2] [3] [4] |