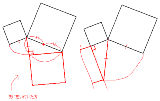
このような配置を連想させるヒントではないかと
数学@ふたば保管庫 [戻る]

|
方べきの定理による解法発見 因数分解で 積=積 にしてた なるほど |
|
a<bとして 半径bの円Oを書いて半径をOPとする。 OP上にOQ=aとなる点Qをとり、Qを通るOPの垂線を引く。 その垂線と円の交点の好きな方をRとすればQRが求める正方形の一辺。 ∵方べき 一頂点を共有してる理由が分からん |
 このような配置を連想させるヒントではないかと |
|
【高校受験2015】千葉県公立前期<数学>講評…時間配分がポイント 2015年2月13日(金) 12時22分 http://resemom.jp/article/2015/02/13/22885.html > (5)の作図は、三平方の定理の応用や、円を利用して直角をつくることが求められるなど、受験生にとっては解法に気づきにくいものだったと考えられます。 「円を利用して直角をつくる」ということは、やっぱり円周角の発想につかまった感じかな。 |
|
2015首都圏公立高校入試 > 千葉 > 数学(前期) http://www.tokyo-np.co.jp/k-shiken/15/cba/cba1/cba-su/su-a_1.html ここでも半円弧に対する円周角で直角を作ってるな…… 何か自分の方に見落としがあるような気がしてきた…… |
|
あれ?「半円弧」?「半円周」? 辞書にあるのは「半円周」だな。。 |