���w���ӂ��Εۊnj� [�߂�]
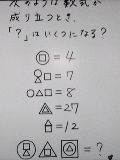
|
4^1=4 1X3+4=7 1+3+4=8 3^3=27 3X4=12 (4X3)^1+4^3+(3^1)^4= |
|
>No.97121 ����ȊO�̓������o�����q�ꓙ�� |
|
���ԓ����肪�Ƃ��������܂����B |
|
���ꂼ��̋L����������\�����ꂪ�����ł��芎�ꌅ���Ƃ���Ȃ�� ���ڂ��ׂ��͂S�Ԗ� �S�Ԗڂ́��ӂ������������Ȃ̂Łu�R�̂R��v�̂� �P�Ԗڂ́Z�Ɓ����Ⴄ����������u�P���R�v���u�T���P�v���u�P��S�v���u�W���Q�v���u�S�̂P��v�����A�L���̒��ɋL��������W�́u��v�Ɣ����Ă���̂Łu�S�̂P��v�ɂȂ� �����灛�Ɓ��͂��ꂼ��S�ƂP �����S�Ł����R������T�Ԗڂ́u�S��R�v�ŁA�㉺�ɏd�Ȃ�W�́u��v �Q�Ԗڂ͏㉺�ɏd�Ȃ�Z�Ɓ��Łu�P��R�v�Ɓ����S�Ȃ̂Łu�R���S�v�ɂȂ�A���ԋL���̊W�́u���v �R�Ԗڂ͎��̊W���u���v�ŋL���͂��ꂼ��P�ƂR�ƂS |
|
�����ȒP�����邩����ςƂ�����g�����ق��̓����������� |

|
http://2ch.hork.info/res/hayabusa3.2ch.sc/livemarket2/1433056234/82 |
|
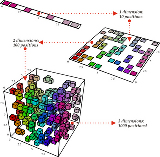
�悤�킩��}�[�W���ő剻���邩�炶��Ȃ��� ���ƃK�E�X�J�[�l�����L�\������ ���Ƌ@�B�w�K�̕���Ō��������̎͋��ʏW�����ۂ̂��Ƃ� �v�Z�ʂƂ͂���܂�W�Ȃ� �������͂��c |
|
�Đ��j�q���x���g��Ԃ��Ė��O����炵����� |
|
�[���Ă��Ȃ܂��@��chokudai�搶�ɕ����� |
|
�ʎq�_�̒m���͗v��Ȃ��B �Ⴆ�ΎR�̏ォ��{�[����]�������Ƃ��ɁA�[�܂Ŗ����H�蒅����͂������ǁA �a��E�݂Ɉ����|�����Ď~�܂��Ă��܂��ꍇ������B ���̂Ƃ�������ƏR����Ă�����A�a��E�݂��甲���o���āA�{�[���͍Ăѓ]����͂��߂�B �Ă��Ȃ܂��@�ł́A�R�������ɁA�M�͊w�̎��ɉ������G�l���M�[��^����B ���x��������ΔM�G�l���M�[���傫��=�R����͂����� ���x���Ⴏ��ΔM�G�l���M�[��������=�R����͂��ア �Ƃ��������B |
|
>�Ƃ��������B �o�J���ۂ����ď��Ȃ��� |

|
���age |
|
>No.96505 >0!=1 �Ȃ�ł��� |
|
�Ȃ����r�b�N���o���I�ȃ��}��������Ȃ� |
|
�K���}���ׂ�B �L�~���m�I���Z���Ȃ�B |
|
�K��̒�`�������ĂȂ��߂Ă݂�B �L�~�����ʂ̍��Z���Ȃ�B |
|
9�H�H�@�I�o�P��9 |
|
�������݂������l�ɂ���č폜����܂��� |
|
>0��0��͂P >1��1����P �����Ă�H |
|
-1^��=-1 |
|
i^i = ����(�������݂���) |
|
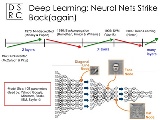
�w��[�������back propagation�ɂ��덷�`�d���w�����I�Ɍ������邩��A�w�K�̌��ʂ��قƂ�nj���Ȃ������炵���B �w��[�����Ă����Ȃ��Ȃ����̂́A�V���Ȏ�@���������ꂽ�̂ł͂Ȃ����낤���B |
|
���ʂ������� |
|
>�w��[�������back propagation�ɂ��덷�`�d���w�����I�Ɍ������邩��A�w�K�̌��ʂ��قƂ�nj���Ȃ������炵���B >�w��[�����Ă����Ȃ��Ȃ����̂́A�V���Ȏ�@���������ꂽ�̂ł͂Ȃ����낤���B �ł�����Deep Learning���o�b�N�v���p�Q�[�V�����g���Ă����Ȃ����������H |
|
�Ă������펯�I�ɍl���ăX�R�A��n���q�̘a�ŕ\�����Ƃ��ɁA ���ꂼ��̈��q���C�ӂ̒l����蓾��i�X�̈��q�ɑ��Ƌ�ʂł�������������j���� �����܂������X�R�A��\��2^n�ʂ肩������̑g�ݍ��킹���ł��Ă��܂� ���̂����̐�����1���炢�Ŏc��͎̂����������Ɍ����Ď��͉ߊw�K�ŁA �V���ȃT���v������͂����瑬�U�j�]���� ��݂����Ƀj���[�����𑝂₷���1���q1�����ʂ̂��厖�A �Ƃ����̂�����܂� |
|
>��݂����Ƀj���[�����𑝂₷���1���q1�����ʂ̂��厖�A ���q���ăj���[�����̂��ƁH |
|
�悭�킩��Ȃ����j���[���������Ȃ��ق��������I���������Ă��Ƃ��낤�� |
|
���ꂾ���A���S���Y�������P����Ă������Ă��Ƃ��낤 ���N�b��ɂȂ���5x5���@�w�̑S�����v���o���� http://resemom.jp/article/2014/03/03/17380.html |
|
�������A���S���Y���̖{����back propagation����i�����Ă��Ȃ���H |

|
��������炢�́� ���������I |
|
�l�p |
 ����B https://www.youtube.com/watch?v=t44qaI7-eHIttps://www.youtube.com/watch?v=t44qaI7-eHI |
 �������悷���� |
|
�V�����Ԃ��Ă���Ǝv�����ǁA �����܂ł����Εϑ����傫���Ƃ�Ȃ���� �����ȕ��ׂ��ł��܂��ˁB |
|
https://www.youtube.com/watch?v=4jHu1tnrsGQ&feature=youtube_gdata_player �T�C�N�������@ |
|
�n�[���j�b�N�h���C�u |
|
���[���[�̎O�p�`�H |
|
���[���b�p�̂ǂ����̍��̍d�݂Ƃ� ��]�h�A�݂����Ȃ̂ɂ��g���Ă��� �����[���[�O�p�` |
|
�^�~�Ƃ����Ă܂��Ƃ܂ǂ��ƓǂޖG���L���� |

|
�p�C�v���Q���T�Ђɐ�Ƃ� �ǂ��������Ƃł��� |
|
�~���`�Ȃ̂Ȃ�n�Ƃ��h���Ď��̏�ł��낪���� �^���Ƃ�Β��ϓI�ł͂Ȃ��H �ł���ΐ���ɕʂȐF�̖n��h���Ă� |
|
�����Ƃ��Ă̓X����̃p�C�v���̉~���A �G�����������ɂ��Đ����������x�X����Ɨǂ��̂��A �t���[CAD�ɓ��͂��鐔�l�̌v�Z���@��m�肽�����B |
|
���r�p�C�v����400�̐��@�͂킩���Ă���H �s�ꐫ���Ȃ��̂ł� |
|
�������݂������l�ɂ���č폜����܂��� |
|
�������݂������l�ɂ���č폜����܂��� |
 >No.97038 |
|
cad�g���Ȃ� �~������������������ arcsin�Ȃ�Ă������ |
|
���ɂ��[���͑厖���� �����Ȃ�ĂȂ� |
|
�C�����Ă悩�����ł��� ����͂Ђǂ��}���Ǝv���Ă��� |


|
�S�l�Z��̖����q�̉��͂P�̎��Ɋ��ɂR�܂ł̉����Z���ł��Ă��� �����ĂQ�|�Q�̓����́w�����x�Ɠ����w�[���x�̊T�O�ɗ����������� �Q�̎��ɋߏ��Ŗ�����R�̂��َq�Z�������͉䖝���ĕ����Ă��ꂽ���ɂR�̂��َq���S�l�ŕ�����Ǝc��́w�����ɂ͂Ȃ��P�x�ɂȂ�ƍl���w�}�C�i�X�x������ ���������N�ɂ͂R�̂��َq�͂��ꂼ����S�������Ă��̂P�Q����S�Â�����Ηǂ����Ƃɍl�����y�ѐ_���Ɛ��ߕ��ꂽ |
|
�R�s�y����Ȃ��̂��R�� |
|
�C���h�N�w�́u���v�𐔊w�ɈڐA������ł��偄�[�� �������̂ق����Ԃ����܂��� |
|
>�A������ˁH ���������Ȃ��ł����� ���������ł����� |
|
>>�A������ˁH >���������Ȃ��ł����� >���������ł����� ���C�[�� �����[�� ����� |
|
0�ȊO�ɂ��������ĂȂ�������ˁH |
|
���t�𐔒l�����Ă��Ȃ� �������t���琶�܂�Ă�݂������� |
|
>0�ȊO�ɂ��������ĂȂ�������ˁH �Ɩ��͌������Ă��� ���Ⓙ�͍������� |
|
���w�Ƀl�g�E���݂����ȃX����͎�����Ȃ��� �h�p�����l������������ ���������l���ăT���N�ȃC���[�W |
|
����ȏ���ȃC���[�W���������Ă����� |
| [0] [1] [2] [3] [4] |