
物理版
数学@ふたば保管庫 [戻る]

|
>光は波なので波長が伸びたり縮んだりするだけ速度は変わらない この説明で納得しちゃうんだ? 走ってる車と停まってる車それぞれの前照灯が同じ速度ならば走ってる車からの方が早く到達する事になるがね |
|
光速に近い場合の速度の合成則はv'=(v+V)(1+vV/c^2)が正しい 普段使う速度の合成則v'=v+Vはv,Vが光速cより十分小さい場合でのみ成り立つ近似則だから車のヘッドライトに適用するのは上の式なわけ Vが車の速さで、vが光速(v=c)とすれば、静止してヘッドライトを眺めた時の速さv'は v'=(c+V)(1+cV/c^2)=c になって光速を超えることはないわけだ |
|
>が正しい >普段使う速度の合成則 >適用するのは上の式なわけ >になって光速を超えることはないわけだ みんなはこんな馬鹿っぽいレスしちゃ駄目だよ♡ |
|
>上記の慣性の法則からいけば走っている車のヘッドライト、つまり光は光速を車のスピードの分だけ超えている事になると思うのです。 若いアインシュタインはスレ主とは逆につぎのように考えた:「慣性の法則」もとい「速度の合成則(ガリレイ変換)」が光にも適用できるとすれば〈手鏡を持った自分が光速で前進した途端に自分の顔の鏡像が見えなくなる〉という事が起こるはずだが、そんな事は”ガリレオの相対性原理“からして起 |
|
(続き)こり得ない。とすれば、光ほどの速さで動く物体についてはガリレイ変換とは別様の変換が適用されるべきであると。 |
|
音波とから波の実体は媒質の疎密とか変移とかで表されるが、 光というのは(真空中を伝わることからわかるように) 疎密とか変移を定義できるような通常の媒質を伝わる波では無く、 動く電場が動く磁場を生み、その動く磁場がさらに動く電場を生み… というマッチポンプで進行する変な波 ここで簡単に「動く」と言ったが、動きを定義するためには (1)時間を最初に定義して動きを導くか、 (2)時間を導くために動きを定義するか、のどっちかの選択の余地が論理的にはあって、 しかし物理学のテーゼの一つな相対性(どこでも物理法則はいっしょ)との兼ね合いとか 実験事実(マイケルソン・モーリーの実験)とかとマッチするのは後者の方だった…! そうなる理由はだれも知らん 光の伝播を説明するマクスウェルの方程式自体は(1)と(2)の立場に中立で、ただ「真空中光速度=c」とだけ逝ってくれる |
|
>手鏡を持った自分が光速で前進した途端に自分の顔の鏡像が見えなくなる〉という事が起こるはず そうなったとして、何か問題でも?とマクスゥエルの電磁方程式を学ぶ前の物理学科の学生なら聞き返したことであろう… スレの話は、光の成り立ちに言及せねば完全な説明にはならないのだ |
|
書き込みをした人によって削除されました |
|
スマンNo.96971の前半のは撤回 No.96968な「速度の合成則(ガリレイ変換)」仮定の下では、 真空中光速度が絶対か否かに関係なく手鏡に普通に自分の姿が映るだろJK (∵さもないと「手鏡に自分が映るか否か」が自分の絶対速度に依存するってことで相対性に反するし、 |
|
> No.79385 ほんとしつこい |


|
π・0.000…1=0.000…1 π=1 |
|
点は円である |
|
二桁は∞か |

|
わかりま線形代数 |
 物理版 |

|
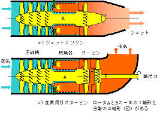
軸が回転してない状態で、燃焼室に直接送風機で圧力かけたとしても 運転時と同様の風の流れになるぞ 始動時の方向を維持するわけじゃない |
 ついでで、ジェットエンジンの風物詩 ショックダイアモンドの解説があったわ |
|
スレ主の高校卒的な静水力学の思考方法では解けないよ 揚力や霧吹きの原理を理解しましょう、そうすれば、なんとなく脳内シミュレーションできる 数学的には、動水力学と圧縮流体をぐぐれ |
|
でた。 適当にそれっぽい言葉を並べて説明しない奴 |
|
>No.96658 説明出来ない時点でオマエはスレ主以下で数学板には要らない子 |
|
流体は流れにくい方向より流れやすい方向に流れようとする性質があります。 ですのでジェットエンジンを設計する際は、吸気口側より排気口側の方に流れやすいように設計します。 スレ画で言うなら始動時に左から右へと流れが出来ており、 すでに流体が左に流れにくい状態になっています。 さらにジェットエンジンの設計が左から右へと流れやすい構造になっているため 燃焼により発生した圧力による流れも左から右へと流れます。 バルブレスパルスジェットエンジンでググルと原理がよく解るかもしれません。 流体の性質を数学的に証明、説明しろというのはさすがに難しいですが。 |
|
理解できても解説が出来ない人や解説できても理解してもらえない人は安易にレスしないでください ぐぐれと命令されると不愉快ですよ |
|
>流体は流れにくい方向より流れやすい方向に流れようとする性質があります。 >ですのでジェットエンジンを設計する際は、吸気口側より排気口側の方に流れやすいように設計します。 ここまでは、問題文を言い換えただけ 以降は、これを根拠として説明したつもりになってるだけ |
|
ターボファンエンジンの動作モデル つべにもあるけど解説米つきなんでニコから http://www.nicovideo.jp/watch/sm23231291 |
|
レベル低い |

|
5分はできるんだろ いくらなんでも |
|
tan(2分5厘)*r*(1-cos(x/r)) x=0~2πr |
|
フリーのCADソフトを使うのは数学板的には邪道? |
|
切り口の展開図の曲線の式あるんだからグラフ書けばいいじゃん |
|
>直径400ミリの円筒形(塩ビパイプvp400)を2分5厘に斜めにカットするための型紙(切り口 塩ビパイプの呼び径(VP400等)の数字イコール実寸じゃないからな。 呼び径400(VP400)の塩ビパイプの外径は基本寸法で420mmで平均値で+-1.3mmくらいの誤差があったはず、なんで実測してから計算した方が良いぞ… |
|
VP-400Aパイプを工場以外でキレイにカットできる方法があるのかどうか疑問だ。 400だとバンドソー使えないし、ノコだと断面がガサガサ |
|
車のナンバーは4桁目に0が使われてるけど、それを排除する理由は? |
|
9*9*8*7=4536 |
|
4桁目は空欄で0表示は無いでしょ、4桁ナンバーが好きなんだ 4536通りかぁ意外と多いな ありがとうです |
|
豆知識
自動車のナンバーは、下2桁の42(死に)と49(死苦、轢く)が欠番。 ただし希望番号の場合はこれらのナンバーも出してくれる。 |
|
希望ナンバーの抽選番号と人気ランキング http://usedtrucks.blog.fc2.com/blog-entry-375.html 抽選対象番号は地域によって違うって知らなかったよー |

|
limit(sin(x)/x,x=0)=1 |
|
0!=1 なんか今日知った。 |
|
定期age |
|
>No.96505 >0!=1 なんでだよ |
|
なんかこうビックリバン的なロマンがあるなぁ |
|
ガンマ関数を調べろ。 キミが知的高校生なら。 |
|
階乗の定義を書いてながめてみろ。 キミが普通の高校生なら。 |
|
9⑨⑨ オバケの9 |
|
書き込みをした人によって削除されました |
|
>0の0乗は1 >1の1乗も1 あってる? |
|
部分集合に最小限が必要なんだっけ むりじゃね |
|
ならば適当に並べればいい |
|
>部分集合に最小限が必要なんだっけ 最小元な つまり半無限区間(を含む部分集合)だと順序化できないと言いたいようだが 任意の実数の部分集合は 必ず有限長の閉区間の線分(たとえば[0,1])に1対1で射影できるんで 射影してから普通の不等式で順序化すれば何の問題も無いよね |
|
開区間と閉区間は同相ではないけど全単射はつくれるのか なるへそなるへそ |
|
>任意の実数の部分集合は >必ず有限長の閉区間の線分(たとえば[0,1])に1対1で射影できるんで それ、具体的にはどうやるんだ? (-∞、∞)→[0,1] の写像を具体的に示してくれないか? |
|
1/2 + (tan^(-1)x)/pi |
|
それ開区間じゃない |
|
>必ず有限長の閉区間の線分(たとえば[0,1])に1対1で射影できるんで >射影してから普通の不等式で順序化すれば何の問題も無いよね それだとさ Rの任意の部分集合A_λに対して[0,1]への射影f_λが存在して、f_λを使って定義されるA_λの順序関係≧_λがあるわけだよね それって整列順序の定義として問題ないのかな つまりA_λは順序関係≧_λのもとでは確かに最小元が存在するけど部分集合ごとに全然違う順序関係を使っていいのものなのかな |
|
射影しつつ無限遠点を加えてコンパクト化するのは 「無限」の扱い方では割と常識だと思うのだが |
|
>射影しつつ無限遠点を加えてコンパクト化するのは >「無限」の扱い方では割と常識だと思うのだが それは確かに誰でも知ってる常識だが、この話と関係するのか? |
| [0] [1] [2] [3] |