
微積分さんまじかっけえ
数学@ふたば保管庫 [戻る]

|
割合は想像に依存する |

|
零が無ければあんたはここに書き込んでなどいられない |
|
>もし見付からなかったとしたら「0」は今ごろ何をしているのだろう 就活じゃね? |
|
4人兄弟の末っ子の俺は1歳の時に既に3までの加減算ができていた そして2−2の答えは『無い』と答え『ゼロ』の概念に理解を示した 2歳の時に近所で貰った3つのお菓子を長兄が自分は我慢して分けてくれた時に3つのお菓子を4人で分けると残りは『ここにはない1』になると考え『マイナス』を発見した しかし翌年には3つのお菓子はそれぞれを4等分してその12切れを4つづつ分ければ良いことに考えが及び神童と崇め奉られた |
|
コピペじゃないのかコレ |
|
インド哲学の「無」を数学に移植したんでしょ>ゼロ そっちのほうがぶったまげる |
|
>就活じゃね? 働きたくないでござる 勉強したいでござる |
|
>>就活じゃね? >働きたくないでござる >勉強したいでござる やる気ゼロ 収入ゼロ 流石やな |
|
0以外にも見つかってないやついるんじゃね? |

|
すなわち、数学とは物の存在確率を変動させる術である |
|
共感覚みたいな |

|
表面積 裏面積 合わせて両面積 |
|
いつでもどんなときでも微分積分だよ |
|
間違えた 俺が信じられないのは 球の表面積が 4πr^2 ってこと これによく気が付いたと感心した |
|
まず円柱から円錐をくりぬいた図形から球の体積Vを求める 次に球面を細かく三角分割しそれらを底面に持ち頂点が球の中心と一致する三角錐に球を分割する 球の体積Vを三角錐の体積の総和として表すとV=Sr/3となって体積から表面積が求まる 微積分のありがたみを感じる |
 微積分さんまじかっけえ |
|
区分求積すればすぐに出るよ |
|
学校教育も公式だけじゃなくて そこに至った経緯とか あるいはなぜそうなのかという詳しい解説も教えるべきなんだろうけど 前に話題になった小学生なら教わらなくてもわかっちゃうんだろうな |

|
テスト |

|
数学はナイフ 数学者は、ナイフそのものを、作ったり、切れ味をみる。 物理屋は、ナイフで、物を切ったり、削ったりしてる。 化学屋は、ナイフで切ろうとしてるが、いまいち。 生物屋は、ナイフがさやの中に・・ |
|
経済屋はナイフを大剣と言い張って使いこなしてる振りをする。 |
|
化学屋や生物屋はナイフ使えるようにするためにまず分厚い殻をハンマーでわらなあかんねん 経済屋はナイフを実演販売 |

|
話がすごい方向に |
|
>次に『等しい確率』は断定表現なのでおかしい >『同様に確からしい』が正しい >ただしこの文章においては『同数』で充分 わかったのかい?お馬鹿さん |
|
>ただしこの文章においては そうだな この設問においては、正しいな 普通、買うって言ったら買った傍から補充するとは考えないからな |
|
>この設問においては、正しいな この設問においては、な No.96626は広義においての意味に拘る頭の固い子なんだろうな |
|
自演でした |
|
>自演でした やっと認めたか もう二度とするんじゃないぞNo.96810 |
|
早く子のスレが消えてくれと手を摺り合わせて嘆くNo.96810 |
|
そうそう バカな奴は書き込みしないで欲しいよな 自分を省みない奴とか |
|
>No.96626は広義においての意味に拘る頭の固い子なんだろうな それにしてもしつすぎる 病気だな 生まれはどこなんだろうな |
|
>早く子のスレが消えてくれと手を摺り合わせて嘆くNo.96810 蠅はNo.96626とNo.96628だなw |

|
y=floor(x/2)+1 floorは床関数 |
|
y={(2x+3)+(-1)^x}/4 |
|
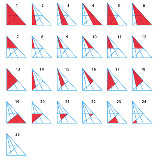
25は何なんだ? |
 25は左上の黒い三角形です。 |
|
25がありなら30までいけるやろ |
|
25はひどいな |
|
25がありなら線上は全て微小な三角形の集合ですって言い切れてしまうではないか |
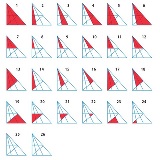 本文無し |
|
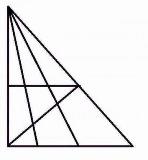
【問題】この中に三角形はいくつあるでしょう(25個以上でGoogle社員の素質あり) ってやつだけど、ソースが見つからない。どうやらネタらしい。 |
| [0] [1] [2] [3] |