本文無し
数学@ふたば保管庫 [戻る]
|
1 |
|
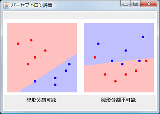
1次元の場合から数えてみれば |
|
分離って一つずつにするのか? nに依らず1通りだろ |
|
ごめん >n-1次元平面 こうだった |
|
d次元空間の一般位置にある(←重要)d+1個以下の点は d次元空間における超平面(それ自体はd-1次元)で 任意の組み合わせでの分離でいける (例:平面上の一般位置にある3点は直線の引き方次第でどうとでも分離でいける スレ問はn次元空間に対してn点なので、全部一般位置なら Σ[i=0..n]n_C_i通りの分離がでいける (平面に対する符号の違いも区別 |
|
↑間違ってるよ 簡単にして2次元平面で考えてみたらどう? |
|
勘違いすまん n次元にn個の点か |
|
>点の集合{(d1,...,dn)|di∈{-1,1},i∈{1,...,n}} 2^n個の点だよね? |
|
では次にリーマン幾何空間で考えてみよう |

|
>線は1次元点は2次元 Name 名無し 15/02/08(日)05:24:38 >圧縮して形が変わるのが2次元 >変わらないのが1次元 小学生が良くそういう発見をするよね |
|
2次元はエロゲやアニメに登場する女の子 3次元はリアルJK等現実世界の女の子 |
|
うんこ |
|
del |
|
スレッドを立てた人によって削除されました |
|
スレッドを立てた人によって削除されました |
|
スレッドを立てた人によって削除されました |
|
スレッドを立てた人によって削除されました |
|
スレッドを立てた人によって削除されました |
|
スレッドを立てた人によって削除されました |
|
スレッドを立てた人によって削除されました |
|
なんでそんなに相手の言うことを否定したがるのか分からない ネットだから? |
|
相手が間違ってるのだから非難するのが当然、という考えの人はわりと多いのよね そういう人が自分の間違いを指摘されると非難されたとおもって暴れだしたりする ネットでよく見るけどリアルでもよくある話 |
|
No.96074 No.96332 結局同じ答えに戻ってきたのな |

|
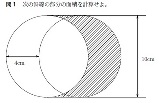
ベイズの定理を使えば10/49らしいが どう考えても1/4 |
|
お前それ1回目見なかったあとに12回連続ダイア引いてからでも同じこと言えんの? |
|
ああ、13回って言えばよかった。後悔 |
|
最初の一枚だけ引いたとき、ダイアである確率は13/52 その後3枚のダイアが出たとすると箱の中のカードがダイアである確率は10/49 仮に3枚のカードがダイアのJ.Q.Kであったとして考えてほしい 残っているカードは ダイアの1〜10 ハートの1〜K クラブの1〜K スペードの1〜K の49枚でそのうちダイアは10枚 よって10/49 ダイアのJ.Q.Kが出た時点で、箱の中のカードはダイアのJ.Q.Kでは必ずないってことが大切 |
|
事後の操作により事前の結果が変わるというのが理解できないだけ。事後に3枚ダイヤが出ようが12枚ダイヤが出ようが最初に1枚引いた時点で13/52だろ。さすがに事後に13枚出た場合は0だろうけど。 |
|
柄が全て不確定なカード52枚から 最初に1枚引いたカードだけなら ダイヤの確率は1/4でいいのさ その後、 残り51枚のカードのうち3枚の柄がダイヤであるという 情報が開示されて確定したので 最初のカードの柄がダイヤである確率も、 その情報によって不確定性が減って変化するわけよ もっと極端な例をだせばわかりやすいが 3枚じゃなくて13枚引いてそれが全部ダイヤだったら 最初にひいたカードがダイヤである確率は当然0になるわけだ |
|
>そして、残りのカードをよく切ってから 最初はシャッフルしないしカードを選ぶ段階で表を見ないとも書いてないから、 ダイヤを見て選んで、それから設問通り表を見ないで箱にしまえば 100%ダイヤじゃね? |
|
>見て選んで 見て選んでもダイヤを選ぶ確率は1/4 |
|
新品のカードだと順番が決まってるから、 シャッフルせずに1枚抜くところに意味があるのかな? |
|
なぜこんな馬鹿が数学板にいるんだ? |
|
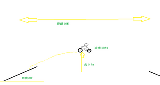
着地の問題だから スタート地点は無視でいい |
|
>タイヤやフレームの弾性、空気抵抗は無視とする ないと無限大にならない? |
|
Oh No〜 w |
 本文無し |
 結果はこんな感じだろ |
|
そうならない原子1個分も歪まないって前提だろ |
|
もろもろ無視するんなら最高到達点から着地点まで落下するだけの話 5m落下したのとおなじ衝撃になる 当然衝撃は重量によって変わる(変わらないのは速度) |
|
無視したら重量に関係なくゼロ除算がどこかで発生するんじゃないの? |
|
問題を 衝撃は何G? → 重力は何G? |
|
速度って書いてあるけど、矢印がかかれていないのはどういうことなの。 |
 かり |
| [0] [1] [2] [3] |