数学@ふたば保管庫 [戻る]

|
オリジナルの電磁方程式で解いても同じ結果になるの? |
|
相対論が出た後でも運動法則が全否定されたわけじゃなくて 近似値としては正しいわけだから 相対論を超える理論ができても 相対論が全否定されるわけじゃない |
|
>謎 >間違い >超えて |
|
http://homepage2.nifty.com/eman/math/group_vel.html |
|
あほう。 |

|
書き込みをした人によって削除されました |
|
結局 3000円の場合 こちらは、店員のちょろまかし200円は+で計算 3000-(300+200)=2500 2700円の場合 こちらは店員のちょろまかし200円は−で計算 2700-200=2500 このふたつを、ごちゃ混ぜにするから おかしいのか |
|
馬鹿の癖に馬鹿にされたからって削除すんな馬鹿 |
|
「和算に恋した少女」にも似た様な話しあったな |
|
2700円から200円引かなければならないところを 足してしまっただけなんやな 悲劇やな |
|
これは 何度も貼られるけど 心理学のもんだいかねぇえ |
|
これ貸借対照表の問題にしてもいいんじゃない |
|
店員が正直者で500円返してしまったら その500円をどう分配するかで客3人が気まずい空気に… 楽しい旅行が台無し。 300円返せば 客「おまけしてもらった−」いい気分 店主「お客に喜んでもらえたろう」いい気分 店員「200円もうかったー」いい気分 三方丸くおさまる。これを世知と言う。 |
|
>世知 盗人が自分に都合よく解釈 |
|
こ、この理屈だと、き、客は2700円の商品と300円のおつりを受け取っているから 店員のちょろまかした200円を足すと、ご、合計は3200円にならないと、だ、ダメなんだな |
|
i が虚数単位ならそうだね |
|
>No.94840 矢印の向きが間違ってるよ ↑じゃなくて→だろバーカ |
|
スレ文見て、雨の中を歩くのと走るのとでは どちらが濡れるかって質問を思い出した。 走る方が濡れなかったよな。 というか、限りなく遅く歩いたらどうなるか 普通の頭があれば分かる。 |
|
>どちらが濡れるかって質問を思い出した。 >走る方が濡れなかったよな。 走る距離と歩く距離が同じ場合ですか? 走る時間と歩く距離が同じ場合ですか? |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
>No.94849 立方体が地面に沿って滑るように動く場合、 雨の落下速度がvとして、 速度vで動くときが雨粒視点での投影面積が最大化されるので 単位時間あたりに受ける雨粒の量の多さで言うといちばん濡れる それより遅くても早くても単位時間あたりに濡れる量は減る モノリス(辺の長さが1対4対9)が最も長い辺を地面に垂直にした状態で、 最も短い辺の方向に動く場合は v√(1^2+9^2)のときが単位時間あたりに濡れる量が最大 球体なら歩こうが走ろうが単位時間あたりに濡れる量は変わらない(vで決まる) 以上のことから、移動者が球体であれば、距離dを歩くよりも走り抜けた方がトータルの濡れ量を抑えられるというのが真だがそれ以外の場合はそうとも言い切れない |
|
>というのが真だがそれ以外の場合はそうとも言い切れない w |
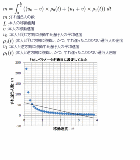 All you see is what you get. |
|
↑移動速度が遅ければすれ違う人数が増えるに決まってるよな 直感通りだわ |
|
他人が一様にあらゆる向きに動いてるときと 他人が止まってるときとでは 結果は一緒なんだろうか |
|
>94744 だと思う |
|
つ[ill-posed] |
|
また馬鹿が出てきた! |
|
>また馬鹿が出てきた! どのレスNo.のどのコメントに対して なぜ「馬鹿」としたのかの根拠なり判断基準なり 示したらどうよ? ん? |
|
キミは馬鹿じゃないから安心して! |
|
馬鹿は死んでいいよ |
|
>馬鹿は死んでいいよ ぉぃぉぃ、ジサツしちゃうかい? ん? |
|
プププ |
|
書き込みをした人によって削除されました |
|
http://curazy.com/archives/42747 やってみよう |

|
100群あたりまで縦に並べて書いていけば気がつく |
|
学校行ってないのか? |
|
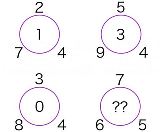
第n群に関して ・第n群は何項入るか。 ・第n群初項は数列全体では何項目か。また値は何か。 ・第n群末項は数列全体では何項目か。また値は何か。 ・第n群第k項は数列全体では何項目か。また値は何か。 ・第n群の合計はいくらか。 とりあえずこれら求めとけばなんとかなる |
|
(1) n^2-(n-1) (2) n^3 |

|
【MOD】なんかいい絵だ!!【わる2】 |
|
-1の27乗 =(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1)x(-1) =-1 |
|
(-1)^27 = -1* (-1)^26 = -1* 1 = -1 |
|
-1^27=(-1)^(2×13+1) =(-1)^(2×13)×(-1) ∵指数法則 ={(-1)^2}^13×(-1) ∵指数法則 =1^13×(-1) =1×(-1) =-1 |
|
ボケはないんかい。 |
|
-1^27=-(1^27)=-1 |
|
>18日5時間38分10秒経過 |
 本文無し |
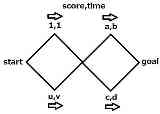 こんなグラフですら経路決定は相当複雑に思える |
|
最小費用流問題は参考にならんかね たとえば http://dopal.cs.uec.ac.jp/okamotoy/lect/2013/opt/handout13.pdf |
|
最大効率経路の部分経路が最大効率経路になってないからそのままじゃDPは使えない とりあえず以下↓の性質を使ってどうにかするしかなさ気 ・任意の正の実数 s,t,s',t'に対して s/t < s'/t' ⇔ s/t < (s+s')/(t+t') < s'/t' が成立 ・従ってグラフの中で最も大きな効率をもつ"辺"を(s,t)とすると、任意の"経路"の効率はs/t以下 |
|
シャボン玉作戦は? |
|
UCBでモンテカルロすればいいんジャネーノ(適当 |
|
クラスNPなのかと思ったけれど 解が本当に解なのかを確かめるのも多項式時間じゃできなさそうだからNPよりも難しい問題なのかな |
|
パソコンが嫌いな計算そう |
|
スコア=総得点 |
|
最短経路求めるなら駅スパート法でいいじゃないの? |
|
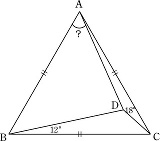
確かに作図が出来ますので答えは出てくる はずですね。ヒントはそういうことです。 |
|
問われてる角度が整数になることも確かじゃないのに、製作者はどうやってこの問題を生み出したん? 適当に角度決めただけじゃ綺麗な問題にならないでしょ |
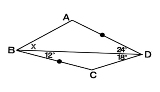 例えばこの問題は正五角形と正三角形からなる図形を元ネタにして作られてるけど、スレ画はなんか元になる図形はあるの? |
|
心配無用 正弦定理と予言定理を有限回適用すれば答えに辿り着くことは保証されている |
|
スレ画ってめちゃくちゃ難しいの?各ABCの角度わかってるよね |
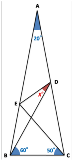 >スレ画ってめちゃくちゃ難しいの?各ABCの角度わかってるよね ラングレーぐらいには難しい |
|
解答 http://www.gensu.co.jp/saito/challenge/a16.html |
|
スレ画両方12°とか両方18°でも解けるの? |
|
両方同じなら簡単か じゃあ12°と6°とかで |
|
ラングレーの問題の変種では |

 穴があったら覗きたいのは 人間の本能的な欲求 |
| [0] [1] [2] [3] [4] [5] |