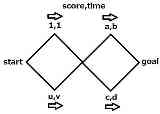
こんなグラフですら経路決定は相当複雑に思える
数学@ふたば保管庫 [戻る]
|
効率が悪い経路でも それが短時間で済むならば ほとんど障害にならないっていう感じか |
|
>効率が悪い経路でも >それが短時間で済むならば >ほとんど障害にならないっていう感じか 言いたいことはあってる 「効率」って語をスレで違う意味で定義しちゃったから 正しくは >スコアの和が悪い経路でも >それが短時間で済むならば |
|
>効率が悪い経路が最大効率経路の部分に含まれていても >それが短時間で済むならば >ほとんど障害にならないっていう感じか もしくはこういう意味かな |
|
気づいたけど 効率がxの閉路が到達可能な場所にあったらそこを無限回繰り返し通ることで 任意のノード間の効率もxに限りなく近くできる だから問題の本質は最大効率の"閉路"を求める事ですね… |
 こんなグラフですら経路決定は相当複雑に思える |
|
最小費用流問題は参考にならんかね たとえば http://dopal.cs.uec.ac.jp/okamotoy/lect/2013/opt/handout13.pdf |
|
最大効率経路の部分経路が最大効率経路になってないからそのままじゃDPは使えない とりあえず以下↓の性質を使ってどうにかするしかなさ気 ・任意の正の実数 s,t,s',t'に対して s/t < s'/t' ⇔ s/t < (s+s')/(t+t') < s'/t' が成立 ・従ってグラフの中で最も大きな効率をもつ"辺"を(s,t)とすると、任意の"経路"の効率はs/t以下 |
|
シャボン玉作戦は? |
|
UCBでモンテカルロすればいいんジャネーノ(適当 |
|
クラスNPなのかと思ったけれど 解が本当に解なのかを確かめるのも多項式時間じゃできなさそうだからNPよりも難しい問題なのかな |
|
パソコンが嫌いな計算そう |
|
スコア=総得点 |
|
最短経路求めるなら駅スパート法でいいじゃないの? |