数学@ふたば保管庫 [戻る]
|
移動にかかる時間が長ければ長いほど多くの人とすれ違うのでは? |
|
問題をうまく設定してそれをはっきり示していただけませんか? 何かの思い込みからかスッキリ納得できなかったんですが、そういわれてみればそんな気もしてきましたが。 現実の道なので、通る道は脇道があることも想定しているのですが、 もし、自分以外の人の数が有限だったり、それぞれの人が通る回数が有限だったりしたときで、かつ、自分がとても遅いときは、自分がスタート地点付近にいる間に、すれ違いうる他のひとが全て通り尽くしてしまうのではないかと考えたりもします。 自分の寿命が有限なので、ある場所からある場所にたどり着くためには速度を遅くするのに限界があり、その範囲で最も遅い速度の場合が、より多くの人とすれ違いうるということでしょうか? それならば自分の寿命だけが無限出会った場合は、どうなるのでしょう。とんちんかんなことを言ってるかもしれないですが、何かあればご指摘いただけると嬉しいです。 |
|
雨に日に早歩きと遅歩きでどっちが濡れるかって実験を見たことあるな、結果忘れたけど |
|
最初に「現実世界で」と書いてあるから関係する要素が無限にあって設定は無理。100円のリンゴを5個買ったら500円だろうが割引されて450円になったけど消費税が.....みたいな。 |
|
移動経路と通行人の密度が同じなら、自分の移動速度で期待値は変わらないです |
|
↑通行人が立ち止まってる設定? |
|
>↑通行人が立ち止まってる設定? 歩いてても同じ 通行人の「密度」が一定なら、すれ違う人数の期待値は相対速度に依存しない |
|
単位時間あたりにすれ違う人の数は移動速度に比例するが 目的地に到達するまでの時間が移動速度に反比例するので すれ違う人数=単位時間あたりにすれ違う人の数×目的地までの時間 は移動速度によらず変わらない しかし気体の分子運動 |
|
>No.94774 密度とは? >No.94775 単位時間あたりにすれ違う人の数は通行人と自分の相対速度に比例するのでは? だからゆっくり歩けば多くの人とすれ違う |
|
まあ拙者くらいの忍びの達人ともなれば 全く人とスレ違わずに目的地に達することも可能でござるがね |
|
>歩いてても同じ >通行人の「密度」が一定なら、すれ違う人数の期待値は相対速度に依存しない あほか? 通行人が皆自分と同じ方向に同じ速さで歩いてたら誰とすれ違うのよ。 |
|
とりあえず一次元の問題にしたらどうかしら |
|
期待値がどうこうって言ってるし 「皆自分と同じ速度で歩いてる」って条件より「全ての人があらゆる方向にあらゆる速さで歩いてる」って考えるべきじゃね |
|
ドレイクの方程式とはちがう |
|
人がうじゃうじゃいるとすれば、分子運動のように考えられるのでしょうかね 分子との違いは道によって全ての人の通る経路が制限されていることくらいですか?大量に枝のついた細い管に気体がある場合を考えれば、経路うんぬんすらも関係無い気もしますが。 一次元化というのは点と線で考えるということだとして、自分が通る経路上の各点について、「各瞬間に他の点がある確率は等しい」と考えれば、遅い方が経路にいる時間が長い分チャンスが多いので、多く出会うということでいいですかね?そもそも「」内の前提が良いのかどうかがわかりませんが... 各点が無限にとれることと各瞬間が無限にとれることが気になります。 また、単位時間の間に同じところに居合わせた点の数の期待値が速さに正比例するのであれば、やはり遅くても速くても同じとなるのでしょうか? いずれも単なる思いつきで仮定していることなので妥当なのかどうかが怪しいですが... |
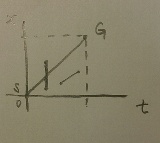 これってもしかして、x-t図に自分の経路を示す線分引いて、そのあと始点終点がランダムな線分を引く問題に帰着されませんか? あとから引くランダムな線分の始点終点の存在範囲が、図の点線内だとすれば遅いほど線分が長くなるけど、線分が引ける範囲が広くて速いときより交わりにくいとかどうでしょう?私には実際に計算できる頭がないので誰かお願いします |
|
上のだと脇道が任意のところにある場合になりますかね? 脇道の箇所に横棒ひいて、そこを始点終点のとりうる場所だとすれば色んな道に適用できませんか? |
|
この問題に似ている
雨の日、歩くのと走るのではどちらが濡れないの? http://matome.naver.jp/odai/2137605451111474901 |
|
この問題は、単純化すると…水道管を水が一定の圧力を受けて断面一杯に流れている(速度V1) 水道管に針金を巻き枠を作り、水の流れの逆向きに移動させる。(移動区間:L、移動速度:V2) Q.針金の枠の断面を通り抜けた水量は?(断面積:S,水量:M) と言う問題だと思う。 よって、 M=abs((V1+V2)*(L/V2)*S = (V1*L*S)/V2+(L*S) ここでA=V1*L*S,B=L*Sとおけば M=|A/V2+B| ↑をグラフにするとよいと思います。 ただし、すれ違いと言うのは、追い越しもあるのでV1が負の場合(A<0)も考える必要があるので、V1>0のグラフとV1<0のグラフを合わせたグラフが題意に合う。 また、スレ主は、余りにゆっくりの移動の場合は、人数が増えないことを指摘している。人の密度が同じでも一度すれ違った人はカウントしないと言う条件があるのであれば V1=V10*K*V2(V10:初期値、K:定数(>0)) と考えるとよいと思う。 |
|
速い移動と遅い移動で、どちらが多くの人とすれ違うかは環境次第。 現実的な場合を想定すると言う問題だが、 家から学校に行くまでのような比較的短い時間の場合は、ゆっくり歩く方が多くの人とすれ違うが、 人生の様な長いスパンなら、300人の村でゆっくり歩いて一生暮らすよりも、都会で速く移動したら、1日で300人とすれ違うのは経験的に分かる。だから、問題の設定次第で、速い・遅いのどちらも有利になることがある。 |
|
条件が違うものを比べて何がしたいんだか |
|
>通行人が皆自分と同じ方向に同じ速さで歩いてたら ↑こういう自説に有利な条件を根拠もなく後から持ち出すのが まさに「詭弁の典型」と呼ばれる負け惜しみですね(笑) 一方通行とか、どこから湧いてきたの? キミの脳内の妄想でしょ、そんなもの 通行人が特定の方向に歩いている前提条件なんか 何も無いんだから勝手にそういう条件付けちゃダメです |
|
病的な例外を指摘してくださったありがたい人を石もて追う所行ェ、 |
|
問題の定式化を志す者なら 少なくとも ・通行人の不生不滅 ・通行人の対地速度のアンサンブル平均が0であること ・通行人の対地速度の時間平均が時間によらず一定であること ぐらいは事前に断っても罰はあたるめ、 その上で通行人の密度とは、単位面積あたりに存在する通行人の個数の期待値なのである またすれ違う人数とは、移動者のテリトリーを動線にそって動かしたときの包絡面で仕切られた空間に居る人数の期待値なのである (通行人の対地速度が0だから今だから言える…! |
|
>すれ違う人数=単位時間あたりにすれ違う人の数×目的地までの時間 >は移動速度によらず変わらない これが間違いなのは理解したのかな? |
|
>・通行人の対地速度の時間平均が時間によらず一定であること スマン訂正これでは何言ってるかわからんorz ・通行人の個数が0でないこと ・通行人の分布が場所にも時間にもよらず一定であること ・通行人の対地速度の分布が場所にも時間にもよらず一定であること No.94817の残りのやつと上のやつが満たされた上でなら、 >すれ違う人数=単位時間あたりにすれ違う人の数×目的地までの時間 >は移動速度によらず変わらない は成立するなぜなら通行人の密度に偏りが無く、かつ不生不滅条件と対地速度分布一定の仮定により包絡面で仕切られた空間に対する通行人のINの速度とOUTの速度の差は時間平均が0故に中に居る人数の期待値は包絡面で仕切られた空間の体積だけで決まる、 |
|
ちなみになんで相対速度ではなくて対地速度にこだわるのかというと、 動線とか、動線に沿って動かしたテリトリーの包絡面とか自体は対象人物が動いた端から地面に対して確定していくので、 対象人物が目的地に達するか、出発点に戻って周期的運動を始めた時点で地面に対して完全に確定し、 0以外の対地速度を持ち得ないから |
|
包絡面で仕切られた空間にINする通行人の数は時間とともに増える気がするんだけど違う? すれ違う数ということだからOUTしたからといってマイナスになるわけではないでしょう |
|
INした通行人の累計と言った方がいいのかな |
|
書き込みをした人によって削除されました |
|
>No.94805 答えが分からない馬鹿がたらればの話に発火wwww |
|
>↑こういう自説に有利な条件を根拠もなく後から持ち出すのが >まさに「詭弁の典型」と呼ばれる負け惜しみですね(笑) 何と言うか、救い難いな。色々と。 朝8時ころの、駅から学校への通学路を考えてみるといい。「現実世界」では良く有る話だが。 そもそも一方通行でない対称性のある場合であってもすれ違う人数は違ってくる。(ドップラー効果の勉強で何度も計算したよね。) ついでに言うと、数学を語るのに「自説」という言葉に違和感を覚えないというのが、また、いけない。 |
|
↑負け犬の遠吠えw |
|
>No.94840 矢印の向きが間違ってるよ ↑じゃなくて→だろバーカ |
|
スレ文見て、雨の中を歩くのと走るのとでは どちらが濡れるかって質問を思い出した。 走る方が濡れなかったよな。 というか、限りなく遅く歩いたらどうなるか 普通の頭があれば分かる。 |
|
>どちらが濡れるかって質問を思い出した。 >走る方が濡れなかったよな。 走る距離と歩く距離が同じ場合ですか? 走る時間と歩く距離が同じ場合ですか? |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
>No.94849 立方体が地面に沿って滑るように動く場合、 雨の落下速度がvとして、 速度vで動くときが雨粒視点での投影面積が最大化されるので 単位時間あたりに受ける雨粒の量の多さで言うといちばん濡れる それより遅くても早くても単位時間あたりに濡れる量は減る モノリス(辺の長さが1対4対9)が最も長い辺を地面に垂直にした状態で、 最も短い辺の方向に動く場合は v√(1^2+9^2)のときが単位時間あたりに濡れる量が最大 球体なら歩こうが走ろうが単位時間あたりに濡れる量は変わらない(vで決まる) 以上のことから、移動者が球体であれば、距離dを歩くよりも走り抜けた方がトータルの濡れ量を抑えられるというのが真だがそれ以外の場合はそうとも言い切れない |
|
>というのが真だがそれ以外の場合はそうとも言い切れない w |
 All you see is what you get. |
|
↑移動速度が遅ければすれ違う人数が増えるに決まってるよな 直感通りだわ |
|
他人が一様にあらゆる向きに動いてるときと 他人が止まってるときとでは 結果は一緒なんだろうか |