maximaでやってみた
数学@ふたば保管庫 [戻る]
|
そうだよ、しらんけど |
|
この方法が通用しない場合を定めよ |
|
この方法はすべてに通用する。 よってこの方法が通用しない場合は無い。 |
|
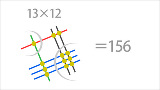
(10a+b)×(10c+d)=100ac+10(ad+bc)+bd 26×73をやってみたら 筆算>上の式>スレ画を描く の順で速かった |
|
書き込みをした人によって削除されました |
|
学生はwikipedia のコピペが普通だろ |
|
>学生はwikipedia >のコピペが普通だろ 文系はそれでいいじゃない?わたしゃ理系だったから詳しくは知らんが、経営学科の奴はそんないな感じって聞いた。 てか、@ウィキのウイルス騒ぎってどうなったか知ってますか? |
|
オイラの卒論は NHKスペシャルをテープ起こししただけ もちろん『ですます調』を『である調』に書き直したけどね それで合格だった |
|
文系の卒論なら他愛無くても大丈夫だが 理系の極ごく一部の卒論はその後発展する可能性がある |
|
よこみち でもノーベル経済学賞て なんなんだろうね |
|
要領の良さという点では企業の求める能力と一致するよな |
|
>要領の良さという点では企業の求める能力と一致するよな 理系工学系だと、他社の特許丸パクリしたりして後でエライことになりそうなので、そうでもなかろう |

|
解答用紙の埋まり方も採点対象なのではないだろうか |
|
普通に1(1)からできないわ x乗はどうやるのか |
|
大学1年教養の問題って感じw |
|
>大学1年教養の問題って感じw 御名答 |
|
90分で全部解く? |
|
>x乗はどうやるのか 対数微分法 f(x) = a^x , aは定数, の微分(導関数)の求め方だが log f(x) = x log(a) と対数をとってから合成関数の微分を使うと d{log f(x)}/dx = f'(x)/f(x) = log(a) ∴ f'(x) = f(x) log(a) = (a^x)log(a) |
|
対数微分法は↑変数のべき乗だけじゃなくて、 関数の積やべき乗の形になってる関数なら大抵使える あと5次までテイラー展開とかキチガイな出題だが こういうのは母関数の方法でも使った方がいいんだろうな |
 maximaでやってみた |
 Mathematicaでズル |
|
宮岡先生の名前をこんなところで見るとは。 懐かしや。 |

|
スレ画の答えは3分の2じゃないの |
|
ここの住人はもう少しスルーすることを覚えないとだめじゃねえか? 揚げ足を取ることに夢中になってもしょうがない |
|
>ここの住人はもう少しスルーすることを覚えないとだめじゃねえか? まあ確かにw 数学板で一般的の話してもなw |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
>スレ画の答えは3分の2じゃないの その通り スレ画は『クイズRPG 魔法使いと黒猫のウィズ』のゲーム画像 このクイズゲームは基本は四択形式で正解を一つ選択するタイプ(※4択で正解が必ず1個しかない) なのだが誤問題が多く ・四択に正解が無い ・四択に正解が複数ある ・正解が不正解で不正解が正解の問題がある ・問題作成時は正解でも時間による変更で正解が不正解になっても修正されない ・機種依存文字を使用しており文字が表示されない 等がある |
|
>ここの住人はもう少しスルーすることを覚えないとだめじゃねえか? あまりにスルースキルなさすぎて荒らしにいい様に付け込まれるだけだよなあ まあ揚げ足取りしてるのが本当に複数いるのかは分からんが、ね… |
|
>スルースキルなさすぎ な人が窘めれてる様を荒らしと呼ぶのか |
|
>スレ画の答えは3分の2じゃないの >その通り するってぇとスレ画は >以上と以下を間違える でいいのか… |
|
>以上と以下を間違える 以上と以下を取り違えているって意味だったなら 2分の1じゃないの |
|
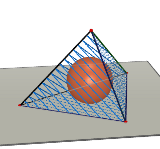
体積をV,表面積をSとすると内接する球の半径rは r = 3V/S 作れる三角錐の種類は対称なものを同じと数えて12通りかな? 12通りなら手計算で全部計算できないことはないけど、う〜ん |
|
平行四辺形のある角に注目して、隣接しない角に線を引くと切断された小片は元の面積の1/2 次元を上げて 平行六面体のある角に注目して、隣接しない角に線を引くと切断された小片は元の体積の1/3(四角錐) 次元を上げて 4次元平行立方体のある角に注目して、隣接しない角に線を引くと切断された小片は元の体積の1/4になる? |
|
隣接しない角では条件が緩いのか 平行になっている-1次元要素(平行四辺形なら上辺、六面体なら上面)のある角に注目して、 対面する-1次元要素の、隣接しない角へ引いた線によって切断された小片 |
|
数学板は機能してないのか… |
|
積分してみたら? |
|
>積分してみたら? 12通りの全部について積分するってこと? |
|
(4,6,8)で三角形を作り 4と12、6と9、8と10をねじれの位置にすると 1.09230324172553とかほんとか |
|
え?そんな小さいの? |
|
体積が34.7846549820783 表面積が95.5357092792151とか 言われた。誰か確かめて |

|
小学1年生 |
|
真面目にお願いしやす |
|
大学1,2年生向け。 4年になるころには皆卒業して、Ann. Math.のような古い雑誌を読むようになる。 |
|
あんまり読んだことないからわかんないけど 各月の目次をHPで確かめる限り、レベルの差がまちまちだけど登場する単語は学部3年〜修士博士レベルまで視られるかなぁ 最新号なんかは微積、線形特集っぽいけど・・・ でも恐らくだけど修士や博士レベルのテーマでも雑誌なんだし初学者にもわかりやすく書かれているとおもうよ |
|
あっ、学部三年での到達レベルを複素解析、常微分方程式、確率論、統計、解析学、線形代数、多様体、測度論、位相空間、群環体を一通り学んでる仮定にしてます |
|
どうでもいいんだが >『態ぁみろ』なんて日本語はない この通りだね 何を踏ん張ってんのかね? |
|
ごめん、まじめにわかりません >ざま【▽様/▽態】 >様を見ろ 辞書にこう書かれていても「態を見ろ」はないことになるの? |
|
学力と資金があっても生きる努力をしなければ出世はしないでしょw |
|
>辞書にこう書かれていても「態を見ろ」はないことになるの? どの辞書の何処にも『態を見ろ』とは書いてありません 「はやい」を辞書で引いてご覧なさい >はや・い【早い/速い】 と書かれているが「諦めるのはまだ速い」とか「川の流れが早い」とは書かれていないでしょ? |
|
>学力と資金があっても生きる努力をしなければ出世はしないでしょw するかしないかではなく出来るか出来ないかだから なんで半笑いなのか知らんけど |
|
>どの辞書の何処にも『態を見ろ』とは書いてありません A=B(ざま【▽様/▽態】)、A=C(様を見ろ)の時、 B=C(態を見ろ)と明記されていなければ、 B=C(態を見ろ)は偽である と言ってる?語源原理主義は横に置いといて |
|
>(ざま【▽様/▽態】) は >A=B ではない しつこいだけの馬鹿は鬱陶しい |
|
>A=B(ざま【▽様/▽態】)、A=C(様を見ろ)の時、 >B=C(態を見ろ)と明記されていなければ、 >B=C(態を見ろ)は偽である オマエいい加減にしろよな! No.92153さんのレス読んだのかよ?! 解らないからって粘着するのは荒らしだかんな! |
|
>学力と資金があっても生きる努力をしなければ出世はしないでしょw お前は何があっても文句ばっかり言って全てを無駄する人間だよ |
|
潤沢な資金さえあれば地位はお金で買えます お金に困らない生活が私のとっての成功なので 資金だけあれば努力も学力も不要です お金を騙し取られない学力程度は必要だけどねw |

|
スレ画のおねいちゃん が どうやって、ケーキの大きさを”同じ”と 証明するか、楽しみでもある・・ |
|
≪姉弟で平等に分割する方法≫ 姉に姉と弟の分を切り分けさせて 切り分けられたケーキから弟が選ぶ |
|
お姉ちゃんのお皿が既に大きい点について |
 また絶妙に切り分けるのにギリなサイズの刃渡りだな |
|
おお 皿の大きさとケーキの割合を考えると 同じとかw |
|
出刃包丁に見えるんだが |
|
この刃のそり具合から出刃はないだろ 洋包丁のステーキ(エマンスール)ナイフだ |
|
最強かどうかは分からないが、今、微分積分を教えるよりも統計学を教えるべきだという主張が米国でなされている。 |
|
数学の勉強ではなく騙されないための勉強じゃないの |
|
書き込みをした人によって削除されました |
| [0] [1] [2] |