数学@ふたば保管庫 [戻る]
|
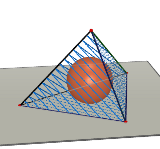
体積をV,表面積をSとすると内接する球の半径rは r = 3V/S 作れる三角錐の種類は対称なものを同じと数えて12通りかな? 12通りなら手計算で全部計算できないことはないけど、う〜ん |
|
平行四辺形のある角に注目して、隣接しない角に線を引くと切断された小片は元の面積の1/2 次元を上げて 平行六面体のある角に注目して、隣接しない角に線を引くと切断された小片は元の体積の1/3(四角錐) 次元を上げて 4次元平行立方体のある角に注目して、隣接しない角に線を引くと切断された小片は元の体積の1/4になる? |
|
隣接しない角では条件が緩いのか 平行になっている-1次元要素(平行四辺形なら上辺、六面体なら上面)のある角に注目して、 対面する-1次元要素の、隣接しない角へ引いた線によって切断された小片 |
|
数学板は機能してないのか… |
|
積分してみたら? |
|
>積分してみたら? 12通りの全部について積分するってこと? |
|
(4,6,8)で三角形を作り 4と12、6と9、8と10をねじれの位置にすると 1.09230324172553とかほんとか |
|
え?そんな小さいの? |
|
体積が34.7846549820783 表面積が95.5357092792151とか 言われた。誰か確かめて |