数学＠ふたば保管庫 [戻る]
|
http://oeis.org/search?q=2016&sort=&language=english&go=Search 好きなのを選んだら？ |
|
8×7×6×3×2 ５は入っていなかった |
|
2016 = 3³+4³+5³+6³+7³+8³+9³ |
|
2×1008 2×2×504 2×2×2×2×252 2×2×2×2×2×126 2×2×2×2×2×2×63 2×2×2×2×2×2×3×21 2×2×2×2×2×2×3×3×7 |
|
藻前らはラマヌジャンか、 |
|
>8×7×6×3×2 8×7×6×(5-4)×3×2×1 |
|
2×（0-1＋6） 4桁の数字はみんな10にしたくならないか？ |
|
>4桁の数字はみんな10に これでいいか？ １⁹＋９¹＝１０ |
|
>これでいいか？ >１⁹＋９¹＝１０ どうせなら10年分作ってくれ 2016 2017 2018 2019 2020 2021 2022 2023 2024 2025 |
|
2016 2*(0-1+6) 2017 2+0+1+7 2018 2+0+1*8 2019 2+0-1+9 2020 20/2+0 2021 20/2*1 2022 20/(√2*√2) 2023 2+0+2^3 2024 2+0+2*4 2025 2*0+2*5 |
|
センター数学は初見問題を出してくる傾向が強くなった それに対処するには圧倒的な実力と考察訓練をしまくる事が必要 |
|
>悪かったなｗ小学校中退でｗ ウケると思ったんだ？これが |
|
>センター数学は初見問題を出してくる傾向が強くなった センター試験で、いきなり過去問に全く無い問題が出て大騒ぎしていたようだな。 ネットでは、対策練れなくてだめだったーという書き込みが多かったが、大手予備校の論評だと簡単で基礎的な問題だという評価もあった。 要するに、定義とか語句の理解の部分を手抜きして、過去問を延々やるのを見透かされたってこったろ。 |
|
>過去問を延々やる 普通これだけでも基礎力はつきそうなモンだがねぇ・・・ |
|
>悪かったなｗ小学校中退でｗ 悪かったね 育ちが |
|
受験するたびにセンターの点数下がるんですが 若さも才能ですかね |
|
若さは間違いなく才能 数学科じゃ25までにまともな論文だせない人は数学あきらめろと言われるそうな |
|
>数学科じゃ25までにまともな論文だせない人は数学あきらめろと言われるそうな 若さは財産だが才能とは思わないな |
|
こちらは数学どころか人生あきらめる状態 まあニセ京都大学生も楽しんだし いっかー |
|
まあ 別にいいんだけど 税金は無駄にすんなよ。 |
|
>タルスキーの円積問題 これと関連するのが「バナッハ＝フォン・ノイマンの定理」で、二次元平面では完全加法測度を満たす通常の面積で考えた場合、円と正方形は互いが「同じ面積でなければ」一方の有限分割と集め直しによって他方に移すことはできない。 では同じ面積ならば、円を分割して集め直し、正方形に移すことができるのかという問は長年解かれなかったが、それが１９９０年になって肯定的に解かれた。 |
|
>要するに分割した断片の次元が整数じゃないだけだろ いまふと思いついた疑問なんだが バナッハ＝タルスキーの定理で 分割した各素片に「連結な」という条件を加えても 成立するのかな？ この定理、非整数次元の有限個の断片に分割するのがミソなんで 非整数次元ってフラクタル図形みたいなやつばっかりだから 連結性なんかなさそうなんだけども |
|
ぶっちゃけさん生きてた〜！！ |
|
>なに鏡に向かってぶつぶつ言ってんだお前 で？オマエはナニ見てそう思ったんだい？ん？ |
|
EMANの掲示板すごいですね |
|
>なに鏡に向かってぶつぶつ言ってんだお前 こういうレスはしない方がいいんだけど それが分からないバカはしちゃうんだよね だからこの手のレスは試金石として便利だ 匿名掲示板だから他人の振りして又荒らすんだろうけどさ |
|
長いブーメランだな |
|
>長いブーメランだな 天唾 ｯﾌﾟｗ |
|
>>長いブーメランだな なに鏡に向かってぶつぶつ言ってんだお前 |
|
書き込みをした人によって削除されました |
|
2分木は、離散連続と無関係では？ |
|
とりあえず以下のように(*)を定義すればモノイドにはなる t * Empty= t t * (BinaryTree u v)= BinaryTree (t * u) (t * v) 自然数から二分木への準同型写像φも定義できるので自然数の拡張とも考えられる φ Zero = Empty φ (Succ n) = (BinaryTree Empty Empty) * (φ n) でも可換則を満たしてくれない 二分木に対して結合則、単位元、可換則を満たすような二項演算は無いものだろうか |
|
完全二分木でm+1個の葉を持つものを数え上げると、 (2m!)/{(m+1)!m!} だから、m→ω（可算無限）としてもその集合全体の濃度は可算だね。 これを非可算にしようとすると、二分木を括弧で表現した時に例えば、 [[…[…]…]] （…は可算無限個の正当な括弧の付け方を満たす） のような、その括弧表記の「子」を取る操作が有限では終わらないものを無数に認める必要がある。 その類全体の要素には親と子が同じであるようなものも無数に現れるから、ラッセルのパラドクスに使われた集合（真の類）の類似物も現れることになるね。 |
 カタラン数の数え上げで二分木と 限定された領域内での格子点を結んだルートを同一視するわけだけど結ぶ点を格子点にかぎらず任意の実数座標の点に拡張したらそれを拡張された二分木と同一視出来ないだろうか |
|
拡張とは、どういう操作なのか定義されてない以上議論できないのではっきり |
|
Kan拡張！ |
|
>。 |
|
ついに堂々と荒らし始めやがった |
|
>日本では貧乏はカスみたいな食事しか取れないが なぜ↑こういう現実と正反対の、変な思い込みがあるのか知らないが 貧困層の方が摂取カロリーが多くて肥満が多いのは、日米欧など豊かな先進国の特徴ですよ 貧乏な国では、そもそも食い物の生産量が足りないので 特権階級以外は普通、肥満状態にならないわけね 時々、海浜国や島国には肥満体の人が多い国があるけど、 実はあれ、産業化されてない状態だと、植民から長くても ２〜３世紀で人口過剰になってリソース食いつぶして 自滅するのです。孤立してる島国は確実にそうなります。 実は日本も鎖国した江戸時代には↑一度やらかしそうになってます 幕府が大急ぎで食生活を変更し、森林を保護し、蝦夷地の資源を 日本社会に導入してやっと何とか助かったんですがね |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
確かに日本の貧困層は炭水化物しか取れなくて太る でそれが何？良い事でも？ 野菜や肉すらも食べられなくて、動けなくて病気にもなって人間らしい生活も送れなくて それが日本の現状 貧乏のアジアとかは貧乏人も野菜や肉を食べてるぞ |
|
>すぐ隣に、人類最高レベルの文明と文化を持つ民族がいて 日本人の代表みたいに言ってるけど コイツは皮脂臭い引き籠りだから 世界のみなさん気にしないでね♡ |
|
叩かれた腹いせに韓国人に八つ当たりしてんのか |
|
最近、匿名板でなぜか相手を特定できてしまう 偉大なエスパー様が増えていますが 完全に誤爆してるぞ、お前（笑） |
|
ほんとにね 国籍透視してる奴なんて「自分は馬鹿です」って自白してるようなもんだよね |
|
保守 |
|
あなたたちは神ですか・ |
|
>なんで「証明すべき事項」が「前提」じゃいかんのじゃ ここまで馬鹿だとは思わなかった |
|
まあ、証明すべきコトが前提として使えるなら、証明なんて必要なく直ぐに正しさは言えちゃうからな。 |
|
標準的な数論を前提とする限り、例えば >3が素数ならば5は素数である という命題は真である ここからは国語の問題になるかもしれないが、 >3が素数であることから5は素数である に、数学的に >3が素数ならば5は素数である という解釈しか有り得ないのだとすると、こいつも真 よってスレの証明もおk オール無問題 （違うというなら「3が素数であることから5は素数である」の数学的別解釈を示してちょ |
|
>No.79385 君は論理学の基礎が分かっていないからメンドクサイが。 古典論理の基礎では演繹による証明は「演繹の分離規則（モーダス・ポネンス）」と各種公理系を組み合わせる。基本は古典命題論理・古典述語論理で共通する。 「演繹の分離規則」とは、(A→B,A)⇒Bという推論規則であり、A→Bを大前提、Aを小前提、Bをそれらからの帰結という。推論規則は論理式((A→B)∧A))→Bとは別物で、大前提と小前提がともに正しければBを証明可能だいうことを意味する。 |
|
(続き） 数学的帰納法の公理は既に他の方が示しておられるが、 >No.100096 >数学的帰納法は以下の公理になっていて >( P(0)∧∀k( P(k)→P(k+1) ) ) → ∀n P(n) とある。 これを公理とする系ではこの論理式は真であり、これを大前提として、小前提を(P(0)∧∀k(P(k)→P(k+1)）とし、小前提が真であると示されれば、 ∀n P(n)を帰結として結論できる。これが証明のモーダス・ポネンスだ。 そしてこのスレの証明では「小前提」が偽である。 (No.100082,No.100112などなど） 言い換えれば、数学的帰納法の公理に演繹分離規則を適用できない。 つまり論理連結記号"→"の定義や論理式型"A→B"の真偽値の議論は的外れだ。 |
|
>No.100161 No.100162 馬鹿を相手にすんな つけあがるだけだろ |
|
いやｽﾏﾝ >▼証明すべき事項 これを読み落としてたわ； >この山から無造作にいくつかの石をつかみ取ると、その中には入るのは同色（白石ばかりであるか、または黒石ばかり）である。 を大前提と言い出した時点で 誰か止めろよ； |
|
>これを読み落としてたわ； 君はこれが多すぎる 自己顕示欲だけは一人前で迷惑千万この上ない >誰か止めろよ； 君みたいに一日中ここに居る訳じゃないんだよ 好き勝手に暴れといてその言いぐさは無いだろ |
|
掲示板でみんなとコミュ取れてると勘違いしてるNo.79385 |
|
>No.100185 ｽﾏﾝｶｯﾀorz 感謝してるﾁｭ♥ |
|
お
題名「お」Name 「ひさし 」E-mai「ぶ」本文「りです」 が正解 |
|
お
ツァー！ |
|
うるせー |
|
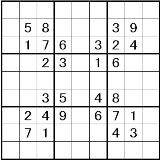
数学が得意な人は数独を見るとラテン方陣を思い出す |
|
ソフトで解けるのは、基本的なロジックしか使っていないヤツなんじゃないの？ それこそ、数学者たちが解きながら論理を作っていった「ｎ国同盟」とか、「X-Wing」とか、「XY-Wing」とか「浜田ロジック」とかは使われていない感じだ。少なくともちょいソース見た感じだと。 |
|
>少なくともちょいソース見た感じだと。 どのソースだね？ ちょっとリンクを張ってみたまへ |
|
http://d.hatena.ne.jp/ku-ma-me/20080108/p1 |
|
数学の得意な人は100まで数えるのが普通の人より 早いと聞くので、こういうパズルも得意だろう 数学をやることによって脳の何かが鍛えれるから |
|
端から順に埋められる数字を埋め続けるだけの安直なプログラムをちょっと前に作ってみたら、2秒くらいで解ける問題もあれば、↓みたいに100秒くらいかかるものもあるとわかった。 http://www.wired.com/2013/01/dr-sudoku-prescribes-a-new-puzzle-for-a-new-year/ |
|
念のためスレ画の問題を同じ条件でやってみたら9秒弱だった。 ↓プログラムの一部 nanpure2__aux(0, _) :- !. nanpure2__aux(N, Ut) :- N1 is N-1, R is N1 // 9 + 1, % 下から上、右から左へ順に埋める C is (N1 mod 9) + 1, chk_fill(R/C,Ut), % R行目のC列目にあるマスを可能な数字で埋める（候補が尽きたら後戻り） nanpure2__aux(N1, Ut). |
|
ありがとうございます |
|
>ソフトで解けるのは、基本的なロジックしか使っていないヤツなんじゃないの？ キリ番おめでとう！ |
|
くそーｗ いちいち傷跡に塩を塗るなよｗ でも、総当たりも良いが、解決のための各種理論を開発できるのが人間と思うけどね。 と言い訳。 |
|
ニュートン法などの反復法によって解を求める手順は ある種の無限級数とみなせるのではないのかね？ |
|
テーラー展開とマクローリン展開じゃダメ？ |
|
>テーラー展開とマクローリン展開じゃダメ？ それらは方程式の数値解法においては、収束を評価する場合には使えるが それ単独で解は導けんだろ |
|
5次は楕円関数とか使うんでしょ知ってる |
|
局所的な縮小写像の数列に持ち込めれば 不動点定理で数列の極限が方程式の解だから 入れ子型の無限積か無限級数の形で書けるようになるよ ニュートン法は↑の特殊な場合 |
| [0] [1] [2] [3] |