
�w�Z�Ŏ��ۂɃT�C�R���g���ėV����Ηǂ���ˁH
���w���ӂ��Εۊnj� [�߂�]
|
1 |
|
�P�����̏ꍇ���琔���Ă݂�� |
|
�������Ĉ���ɂ���̂��H n�Ɉ˂炸1�ʂ肾�� |
|
���߂� >n-1�������� ���������� |
|
d������Ԃ̈�ʈʒu�ɂ���i���d�v�jd+1�ȉ��̓_�� d������Ԃɂ����钴���ʁi���ꎩ�̂�d-1�����j�� �C�ӂ̑g�ݍ��킹�ł̕����ł����� �i��F���ʏ�̈�ʈʒu�ɂ���3�_�͒����̈���������łǂ��Ƃł������ł����� �X�����n������Ԃɑ���n�_�Ȃ̂ŁA�S����ʈʒu�Ȃ� ��[i=0..n]n_C_i�ʂ�̕������ł����� �i���ʂɑ��镄���̈Ⴂ����� |
|
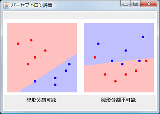
���Ԉ���Ă�� �ȒP�ɂ���2�������ʂōl���Ă݂���ǂ��H |
|
���Ⴂ���܂� n������n�̓_�� |
|
>�_�̏W��{(d1,...,dn)|di��{-1,1},i��{1,...,n}} 2^n�̓_����ˁH |
|
�ł͎��Ƀ��[�}����Ԃōl���Ă݂悤 |

 �w�Z�Ŏ��ۂɃT�C�R���g���ėV����Ηǂ���ˁH |
 �ŋ߂͓d�q�}�l�[������� |
|
����ł���E�݂̐���6�ʑS���Ⴄ�̂ł� �o��ڂ����m���ɂȂ�Ȃ��̂ł́c |
|
������ �Ԃ����Ⴏ�@���Ȃ��� �ǁ[�ł����� �x�C�Y�͐����c���Ă邪w |
|
���w�ȊO�̂ǂ����ŋ����Ă����W���}�C�J�H ���w�̖�肾���č���Ȃǂ̌��ꂪ�g���邱�Ƃ��O��Ȃ� |
|
1. �C�O�ɍs���� 2. �e���������S���Ȃ��ğT�������ɂȂ��� �ǂ��������Ǝv�� �Ō�̏������݂��炷���2�̉\�������� |
|
���w�����A��тʂ��ā@�ł���� �ڂ̑O�ŁA��肷�炷��������� �w�����s�v���� �m�u�t�ł������Ă����邵�Ȃ� |
|
�����ō��Ŗ����������ŏm�u�t�����܂�̂� |
|
���w�̖����������� �l�ɐ��w�������鎖�ł� �K�v�Ȕ\�͂��S���Ⴄ ����Ȃ̐��w�Ɍ��炸������O�̏펯�� |
|
�Ԃ����Ⴏ����ǂ�������ł����� �G���Q�O���ł����� |

|
>����1�����_��2���� Name ������ 15/02/08(��)05:24:38 >���k���Č`���ς��̂�2���� >�ς��Ȃ��̂�1���� ���w�����ǂ��������������������� |
|
�Q�����̓G���Q��A�j���ɓo�ꂷ�鏗�̎q �R�����̓��A���i�j���������E�̏��̎q |
|
���� |

|
>http://d.hatena.ne.jp/hhhhiro66/20091021 ���������̂ɂ͒N���P�`���Ȃ��̂� |
|
������Ȃ��������͂��˂�邯�� �w�͂͏��w�����x�Ȃ��炵�����Ȃ��� |
|
�Q�ƂP�͓����� ����͂��͂�펯�ɂȂ���邩��� |
|
�Q���P�͐��w�̐��E�ł͏펯 |
 �{������ |
|
�����̏Z�l�̃��x������Q���P�̊ԈႢ���ؖ��ł��Ȃ� |
|
�ʂɊԈႢ�ł��������� ���������㐔���������������� |
|
�߂��猩�Ă��邩��킩��Â炢�̂� x-7=19�~x ������Ƃ��� x=-7/18 ���ȁi�h���b |
|
�i���Ȃ��j |
|
>�����̏Z�l�̃��x������Q���P�̊ԈႢ���ؖ��ł��Ȃ� ���No.96135�̎���� a = b�@�@�@�@�@�@�@�@���ӂ�a��������B a^2 = ab�@�@�@�@�@�@ ���ӂ���b^2 ���Ђ��B a^2 - b^2 =ab-b^2�@�@�ň�������������B (a+b)(a-b)=b(a-b)�@�@�����܂ł͖��Ȃ��B ���ɁA(a-b)�������Ă��邪�Aa = b �ł��邽�߁A(a-b) �Ŋ���ƂO����ɂȂ��Ă��܂��B (a+b)(a-b)=b(a-b) a+b=b �܂�A�����̎��̕ό`�͐��藧���Ȃ��B�i�������Ȃ��j ����ĂQ���P�ł��邱�Ƃ͏ؖ��o���Ȃ��B |

|
�P���y���ʼn����� |
|
>No.95833 �X�[�p�[�R���s���[�^�g���ė͋Z�ʼn�����(�炵��) �w�炵���x�ƌ����̂͂܂��R���s���[�^�g��Ȃ��ؖ����@���o�Ă��Ȃ�����B |
|
>�X�[�p�[�R���s���[�^�g���ė͋Z�ʼn�����(�炵��) ���S�̏ꍇ�킯�ɂȂ�Ƃ���܂ł̓g�|���W�[�ʼn��Ƃ������� ����ȏ�͂ǂ����悤�������̂ł����u�S�Ă̏ꍇ�v�ɂ��� �R���s���[�^��Ŏ��ۂɓh���Ă݂ďؖ������� |
|
���N�T�C�G���XZERO�̗ʎq�R���s���[�^���4�F���������Ă��� |
|
�ʎq�A�j�[�����O�Ŏl�F���Ə���Z�[���X�}�����������Ă��� |
|
����Z�[���X�}�����͕��q�R���s���[�^�Ȃ琔�b�ʼn������ |
|
����T���^�N���[�X���Ƃ͈Ⴄ�́H |
|
���͂ɂ����鎞�Ԃ͂ǂꂭ�炢�Ȃ� |
|
�A�[�@�ŏؖ��ł��Ȃ��̂��l�������Ȃ� |
|
>�ʎq�A�j�[�����O�Ŏl�F���Ə���Z�[���X�}�����������Ă��� �ĕ����������ǁA�l�F�����ŏ���͂܂� |

|
>�������Ƃ��ă}�W���X > >����Ȃ̂�邾������ > >�ȏ�i�j �o����Η��R�������Ă��炦�܂����H �Q�l�ɂ������ł� |
|
�������݂������l�ɂ���č폜����܂��� |
|
>�o����Η��R�������Ă��炦�܂����H �o���Ȃ��Ǝv�� �Ƌ��⎑�i���K�v�Ȃ����̂������ɂ���悤�ȃo�J�̋Y���Ȃ̂� |
|
>�o����Η��R�������Ă��炦�܂����H ���O�I�ȗ��R�������A ��w�i�w���ȏ�j�ł���Ă镨���w�Ɖ��̊W���Ȃ�����ł� �����I�ȗ��R�������A ������̏��Ȃ������͍̓_�̎��ɔz�_���炳���̂� �撣���ē��������Ă����Ԃ̖��ʂ�����ł� |
|
�������݂������l�ɂ���č폜����܂��� |
|
�ł͎��͉����������Ǝv���܂����H |
|
>������̏��Ȃ������͍̓_�̎��ɔz�_���炳���̂� ���̕ӂ�͖ϑz���ۂ��������̂��H�� �܂��A�ȒP����������������Ō��ʓI�ɍ������Ȃ����͂����Ȃ� ���������������W�߂����̂���n���Ƃ͎v��Ȃ��� |
|
�����ߒ���(���Z������)�͂����Ȃ��ނ������ł�������Ȃ��H ���Z�������̂��w��I�Ɍ��ĕs���R���ǂ����͒u���Ƃ��ĂˁB |
|
�����Љ�Ă��ꂽ�u�{�Ԃŏ������T�a�U�v�ɂ� ���Ȃ肨���b�ɂȂ��� |
|
>�o����Η��R�������Ă��炦�܂����H �ꉞ�����Ă�l�����邯�Ǔڒ����������� ���O�I�̎g���������������� |
|
del |

|
���R�����������H |
|
������ |
|
�킴�킴�������炢�����炱��������n���Ɠ������� |
|
>>�D�������W�����5���Ƃ�����Ă�l�̓Z���^�[�ō����_�Ƃ��Ċ��ł�C���[�W �Z���^�[�ō����_��点�邱�Ƃ��w���҂̖��߂������ |
|
>���R�������Ă����H ���������Ȃ� �ǂ����� �܂ş���ŃL�[�������Ȃ��̂����H�� |
|
> >�Z���^�[�ō����_��点�邱�Ƃ��w���҂̖��߂������ ���̎���ł͓�����ăZ���^�[�͒��O�ɉߋ���������Ă����������� ����ȂɃZ���^�[�d�v���Ƃ͒m��Ȃ����� |
|
�̂̃Z���^�[���w�͊ȒP��������Ȃ� �]�T�Ŏ��ԗ]������ |
|
2006�N���炾���� ���w������Ȃ��ĕ�������Ƃ�d�l�ɂȂ����̂� |
|
���[�� |
|
�ߑa���Ă�ȁ[ |
|
�X���b�h�𗧂Ă��l�ɂ���č폜����܂��� |
|
�X���b�h�𗧂Ă��l�ɂ���č폜����܂��� |
|
�X���b�h�𗧂Ă��l�ɂ���č폜����܂��� |
|
�X���b�h�𗧂Ă��l�ɂ���č폜����܂��� |
|
�X���b�h�𗧂Ă��l�ɂ���č폜����܂��� |
|
�X���b�h�𗧂Ă��l�ɂ���č폜����܂��� |
|
�X���b�h�𗧂Ă��l�ɂ���č폜����܂��� |
|
�X���b�h�𗧂Ă��l�ɂ���č폜����܂��� |
|
�Ȃ�ł���Ȃɑ���̌������Ƃ�ے肵������̂�������Ȃ� �l�b�g������H |
|
���肪�Ԉ���Ă�̂��������̂����R�A�Ƃ����l���̐l�͂��Ƒ����̂�� ���������l�������̊ԈႢ���w�E�����Ɣ��ꂽ�Ƃ������Ė\�ꂾ�����肷�� �l�b�g�ł悭���邯�ǃ��A���ł��悭����b |

|
�x�C�Y�̒藝���g����10/49�炵���� �ǂ��l���Ă�1/4 |
|
���O����1��ڌ��Ȃ��������Ƃ�12��A���_�C�A�����Ă���ł��������ƌ�����́H |
|
�����A13����Č����悩�����B��� |
|
�ŏ��̈ꖇ�����������Ƃ��A�_�C�A�ł���m����13/52 ���̌�3���̃_�C�A���o���Ƃ���Ɣ��̒��̃J�[�h���_�C�A�ł���m����10/49 ����3���̃J�[�h���_�C�A��J.Q.K�ł������Ƃ��čl���Ăق��� �c���Ă���J�[�h�� �_�C�A��1�`10 �n�[�g��1�`K �N���u��1�`K �X�y�[�h��1�`K ��49���ł��̂����_�C�A��10�� �����10/49 �_�C�A��J.Q.K���o�����_�ŁA���̒��̃J�[�h�̓_�C�A��J.Q.K�ł͕K���Ȃ����Ă��Ƃ���� |
|
����̑���ɂ�莖�O�̌��ʂ��ς��Ƃ����̂������ł��Ȃ������B����ɂR���_�C�����o�悤���P�Q���_�C�����o�悤���ŏ��ɂP�����������_��13/52����B�������Ɏ���ɂP�R���o���ꍇ��0���낤���ǁB |
|
�����S�ĕs�m��ȃJ�[�h52������ �ŏ���1���������J�[�h�����Ȃ� �_�C���̊m���͂P�^�S�ł����̂� ���̌�A �c��51���̃J�[�h�̂���3���̕����_�C���ł���Ƃ��� ��J������Ċm�肵���̂� �ŏ��̃J�[�h�̕����_�C���ł���m�����A ���̏��ɂ���ĕs�m�萫�������ĕω�����킯�� �����Ƌɒ[�ȗ�������킩��₷���� �R������Ȃ���13�������Ă��ꂪ�S���_�C���������� �ŏ��ɂЂ����J�[�h���_�C���ł���m���͓��R�O�ɂȂ�킯�� |
|
>�����āA�c��̃J�[�h���悭���Ă��� �ŏ��̓V���b�t�����Ȃ����J�[�h��I�Ԓi�K�ŕ\�����Ȃ��Ƃ������ĂȂ�����A �_�C�������đI��ŁA���ꂩ��ݖ�ʂ�\�����Ȃ��Ŕ��ɂ��܂��� �P�O�O���_�C������ˁH |
|
>���đI��� ���đI��ł��_�C����I�Ԋm����1/4 |
|
�V�i�̃J�[�h���Ə��Ԃ����܂��Ă邩��A �V���b�t�������ɂP�������Ƃ���ɈӖ�������̂��ȁH |
|
�Ȃ�����Ȕn�������w�ɂ���H |
| [0] [1] [2] [3] [4] |