数学＠ふたば保管庫 [戻る]
 これかな？ http://www.koreatimes.com/article/872100原因は知りたくもないけど韓国人のDNA異常率はほぼ100%だそうだよ俺は専門家ではないからDNAの何が異常なのかまでは分からないけどねでも泥酔した奴が自分を酔ってないと言い張るのと同様に韓国人は自分達が世界一優秀な民族だと自覚してるみたいだねここ数学板だけど板間違えてない？ |
|
スレ主はね もっと他に心配しなくちゃならない事がいっぱいあるよ |
|
>>94145, 94151 2chでそれらの数値を単純に足し合わせて、99%(1%は小数点以下分)のLA韓国人は問題ありとなっている状況を見れば、数学的考察ができていると思えなかったのだが…。趣旨を理解してもらえていないことは非常に残念だ。 この現状を鑑みて、敢えて言うと数学と言う学問は、常に『客観的に事象を分析すること』を目的とするべき学問だと思うが朝鮮・韓国という文字を見るだけでバイアスがかかった思考になってしまうのは、なぜなのだろうか？ |
|
>なんで削除しないんだ？ バカだから削除キー知らないんだよ |
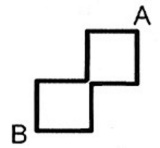 2コマ目は八角形だよなあ |
|
距離が同じ同じかどうかと、 どっちが近いかは、実はまったく答えが異なる。 距離が同じならコーナーが多い方がアウトインアウトで近道できる。 タイトルもショートカットだしな。 |
|
>距離が同じならコーナーが多い方がアウトインアウトで近道できる。 あ〜あ 今度は道路の話 |
|
道のりじゃねーか！ |
|
体積を積分で求めるときにこういう失敗したことあるw |
|
見抜きましたぞ！！！１１ これはフラクタル次元の問題ですな？ |
|
完璧な証明なので誰も反論できないｗ |
|
>完璧な証明なので誰も反論できないw 騙され易いんだね 気を付けた方がいいよ |
|
0.99999････が1ってのと似てる気がする |
|
スレッドを立てた人によって削除されました |
|
スレッドを立てた人によって削除されました |
 ムカついたので削除して置きました。 |
 お遊び掲示板で sage 投稿してる奴って・・・ |
 ガンバレ中二病 つかコテつけるのやめたん？ |
|
おまけ♪うざい！！ |
|
宝くじの1等が無ければ宝くじは存在する価値が無い、 と言うのは一等が無い宝くじは宝くじとは言えないのだから 1等が無い宝くじは宝くじでない、 と言い換えた方が良いのでは… |
|
ていうかいかに一等が稀少な宝くじであっても 全部買えば必ず一等が含まれるのだから 宝くじの一等が当たったからといって一等しかない宝くじなのだと結論づけるのは全くの不合理 |
|
あ ほ う |
|
>No.79385 黙っててくんない？ |
|
トポロジーに出てくる位相不変量はコホモロジーから計算されるものが多い |
|
俺は「手段の目的化」現象に対する数理的考察をずっと長い間温めていた。今も温め続けているが。 数学自体理数系を中心とする科学技術の手段を体系立って目的化している学術科学技術と言える。 |
|
俺は「手段」ごときに振り回されるのは御免だ゜゜゜ |
|
目的化した手段に振り回されない「中庸」。 |
|
行って戻ってくる冒険にはS1構造が入るが 行ったっきりの冒険にS1作用は自然に入らない。 |
|
胞体分割ってチェックポイント全部めぐって一巡して戻ってくる一筆書きの旅だよね？。 |
|
>胞体分割ってチェックポイント全部めぐって一巡して戻ってくる一筆書きの旅だよね？。 輪体だよなそれ。 |
|
d・d=0 二回微分すると消える量は1近傍のメゾスコピックな量。 |
|
全身タイツが破れてなければd・d=0 |
|
層係数コホモロジーよか指数定理 |
|
>なぜこう見えるのか どう見えるんだい？ |
|
つクオリア |
|
クオリアじゃねえ |
 心臓にもないぃ〜 脳にもないぃ〜 どこにも見当たらないぃ〜 こぉこぉろぉ〜 |
|
>どこにも見当たらないぃ〜こぉこぉろぉ〜 「あんたなんか大嫌い。」と叫んでごらんなさい その時傷んだ所にあるんですよ心は |
|
>その時傷んだ所にあるんですよ心は 街中で叫んだらフルボッコにされて体中痛いんですが |
|
>街中で叫んだらフルボッコにされて体中痛いんですが 貴方は体中に心があり愛に満ち溢れている人です そんなひとに嫌いと言われれば 常人も動揺して暴力のひとつも振るうというものです |
 しんどい |
|
これは問題がかなりおかしい。 脳タリンの問題だわ。 |
|
罵倒の仕方が昭和 とか言うといとも簡単に切れちゃうんだろうな 他スレみたいに あとこのお題は数ヶ月前にこの板で既出 |
|
罵倒の仕方が昭和 とか言う奴は常に荒らしてるだろうな 他スレみたいに あと数ヶ月前から粘着してるし |
|
今起きますた |
|
まず出題者がゆとり |
|
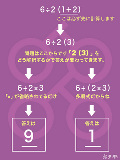
記号じゃないのに×省略するな せめて黒丸つけろ |
|
>No.94081 右のやつ勝手にくくるな |
|
>右のやつ勝手にくくるな くくる前に（２×１＋２×３）としたらよかですか？ |
|
6÷2(1＋2) 6÷2×1＋2 3×1＋2 3＋2 5 |
|
素数を数えるんだ |
|
>ある２人が２から９９までの２つの自然数を考えた。 教えるほうも二人いて、別々に考えてSとPに伝えたんなら 答え出ないんじゃないの？ |
|
>教えるほうも二人いて、別々に考えてSとPに伝えたんなら >答え出ないんじゃないの？ なんで？ |
|
>教えるほうも二人いて、別々に考えてSとPに伝えたんなら 教える方が一人でなければ答えは出ないと言っているのか？ |
|
まず5から101までの数で次の条件をともに満たす値を紙に全部列挙して篩いにかけよ おのずと答えに近づくであろう 1. 素因数が３つ以上の合成数 2. 素数の和で表し得ない数 |
|
4^2+9^2+12^2 |
|
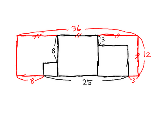
x+(x-3)+(x-8)=25 って考えるけど小学生の場合どうやるの？ |
|
(２５＋８＋３)÷３＝１２ 中央の正方形の一辺が１２ｃｍです。 したがって、１２−８＝４、１２−３＝９ ４×４＋１２×１２＋９×９＝２４１平方センチメートル と教えますね。 |
|
>(２５＋８＋３)÷３＝１２ ナルホドー |
|
馬鹿な俺に >(２５＋８＋３)÷３＝１２ >中央の正方形の一辺が１２ｃｍです 何でこれで一辺の長さが出てくるのか解説してくれ |
 本文無し |
|
>94110 そういう事か 分かりやすかった 3Q |
|
>(２５＋８＋３)÷３＝１２ 真ん中の正方形の左右と下の辺の長さの合計が36cmという考え方もあるな |
|
小4がいっぱい♡ |
|
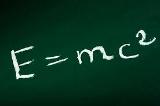
mがキログラムなのが紛らわしい。 10^3×mc^2じゃ汚くなるから？ |
|
すげー |
|
E=mc^2 と E=(1/2)mv^2 の関係をおしえて！ 物質のエネルギーへの変換 ＝物質を光速まで加速したときの運動エネルギーの２倍 ということになるのか？ |
|
E=mc^2 と E=(1/2)mv^2 はそれぞれ別のエネルギー |
|
>効率が悪い経路が最大効率経路の部分に含まれていても >それが短時間で済むならば >ほとんど障害にならないっていう感じか もしくはこういう意味かな |
|
気づいたけど 効率がxの閉路が到達可能な場所にあったらそこを無限回繰り返し通ることで 任意のノード間の効率もxに限りなく近くできる だから問題の本質は最大効率の"閉路"を求める事ですね… |
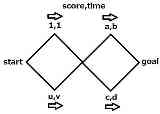 こんなグラフですら経路決定は相当複雑に思える |
|
最小費用流問題は参考にならんかね たとえば http://dopal.cs.uec.ac.jp/okamotoy/lect/2013/opt/handout13.pdf |
|
最大効率経路の部分経路が最大効率経路になってないからそのままじゃDPは使えない とりあえず以下↓の性質を使ってどうにかするしかなさ気 ・任意の正の実数 s,t,s',t'に対して s/t < s'/t' ⇔ s/t < (s+s')/(t+t') < s'/t' が成立 ・従ってグラフの中で最も大きな効率をもつ"辺"を(s,t)とすると、任意の"経路"の効率はs/t以下 |
|
シャボン玉作戦は? |
|
UCBでモンテカルロすればいいんｼﾞｬﾈｰﾉ（適当 |
|
クラスNPなのかと思ったけれど 解が本当に解なのかを確かめるのも多項式時間じゃできなさそうだからNPよりも難しい問題なのかな |
|
パソコンが嫌いな計算そう |
| [0] [1] [2] [3] |