すみません。スレッド立て直します。
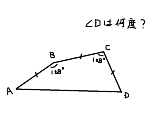
証明お願いします。
以下がいままでの流れ。
| … |
回答１： ∠D＝54° ヒント：△CBDを底辺BDで折り返して菱形CBEDを作る。辺DAを菱形の∠BDEの内角二等分線と見なす。 回答１’： >なんで見做せるのか解らん のであれば、菱形CBEDを作った後で、△ABDを底辺ADで折り返しての凧形ABDGを作ってみよう。 （この凧形ABDGを作ると、等脚台形BCDEもが作るともなく作れる。） |
| … |
回答２： 正五角形に正三角形くっつけて半分にする 回答３（一部編集）： 回答１や回答１’は証明じゃなく「そうなりそう」って発想のみよね 回答２がスマートだけどちょっと導ける気がしない… 回答４（一部編集）： > 回答２がスマートだけどちょっと導ける気がしない… でもこれが答らしい。 ADで折り返すと、正三角形＋正五角形ができるという（実際できる）けど、 それらが「正」三角形と「正」五角形である証明を誰かしてくれ・・・・ |
| … |
図形の一意性よりで何故ダメなのかがわからん |
| … |
 回答３は２つの“話題-評言(topic-comment)”文に分けられる（……だけでなく、スレ自体が２つに分けられてた！）： Ａ）回答１や回答１’は証明ではない。Ｂ）回答１や回答１’（で言い表わされてるの）は「そうなりそう」だという発想のみだ。Ａ）は真（ただ）しい。〈回答１〉は〈当の問題を解くヒント〉だし、〈回答１’〉は〈疑問「なんで見做せるのか解らん」への応答〉だから。Ｂ）は真しくない。〈回答１〉も〈回答１’〉も〈一応「そうなる」のを直前に作図ソフトで検かめた後での「言い表わし」〉なので。因って、回答３がt-c文として真しいのは その論理形式が（ＡまたはＢ）か（ＢならばＡ）のとき、かつ、そのときのみ。 |
| … |
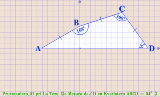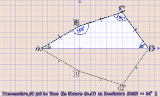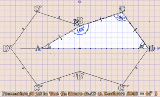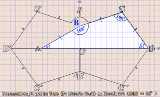
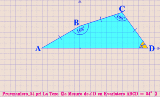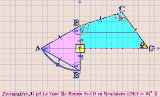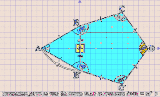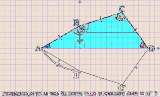
《上で貼った作図アニメについて》 Pruvmaniero_01：〈回答１〉と〈回答１’〉で言い表わした「発想」のアニメ化。 〈菱形CBEDの一辺DE 〉は〈凧形ABDB'の頂角BDB'を成す辺DB' 〉の上に在るべくして在る。 Pruvmaniero_02：与えられた図形〈三等辺四角形ABCD 〉の内に有る〈二等辺三角形CBD 〉を他の３つの象限に対称移動させて〈菱形BDB'C' 〉を視える化したモノ。 そうしたら〈一辺を共有する２つの正五角形〉もが視える化した。 Pruvmaniero_03：垂線と対頂角とを用いて〈直角三角形BDFの１頂角∠BDF 〉としての∠BDAの大きさを得る手法。 この手法は〈論証図〉の形式に書き出しやすい。しかし｛ 四角形ABCDにかんする既定の事柄(Givens) ｝のうちの ｛AB＝BC，AB＝BD，∠ABC＝168°｝が使えてないので、〈この問題についての論証図〉としては不格好になる。 |
| … |
>No.101580の訂正 >「｛AB＝BC，AB＝BD，∠ABC＝168°｝」⇒「｛AB＝BC，AB＝CD，∠ABC＝168°｝」 |
| … |
> 図形の一意性よりで何故ダメなのかがわからん そこが見えないんで、さんすうレベルに噛み砕いてくれると助かります。 |
| … |
BCを起点に考えると図の長さ、角度の条件を満たす図形が一つに定まるのは明らか で次にいきなり正三角形と正五角形くっつけて半分にした図形を用意して、これとそれは同じ図形だよねって言って終わり |
| … |
正三角形＋正５角形はいきなり折り返し図形から考えると大変そうなんで AB=BE,角ABE=60°となる点Eをつくってから考えるとすんなりいくと思う |
| … |
点Eを作ると、正三角形はできる。 ３辺２角までは正五角形と一致する図形もできる。 その先が見えない。 |
| … |
あとはBEの中点とA,Dとの位置関係を考えればOK |
| … |
> AB=BE,角ABE=60°となる点E だから、 > BEの中点とA,Dとの位置関係 とはなんら関係ないのでは。 |
| … |
BEの中点をGとしたとき ∠BAGと∠BADの関係をしらべてみるんだ |
| … |
∠AGDが何度になるかってほうがわかりやすいかな |
| … |
その方面では証明は無理っぽいね。 > 次にいきなり正三角形と正五角形くっつけて これが閃かない限り、答には辿りつけないようだ。 |
| … |
 《回答２の解き方に沿った証明アニメとその解説 》 (00)_与えられた四角形ABCDの頂点Bから辺ADと直交する〈垂線BB'〉を引く。ただし〈BB'＝BF＋FB'〉となるように。(01)_四角形ABCDの頂点Aが在る側に、垂線BB'を'底辺とする〈正三角形ABB'〉を作る。(02)_作った〈正三角形ABB'〉の右側に〈四角形BCDF 〉を辺ADで折り返しての〈正五角形BCDC'B'〉を作る。(*)(03)_手つづき(00)-(02)で以って、求めるべき〈∠Dの大きさ〉は〈六等辺六角形ABCDC'B'の１頂角CDC'の半分〉に等しい事が判かる。(04)_そこで“Ｎ角形の内角の和の定理”を絡めた加減乗除に依って「∠Dの大きさ＝54°」を導く。 |
| … |
> (00)_与えられた四角形ABCDの頂点Bから辺ADと直交する〈垂線BB'〉を引く。ただし〈BB'＝BF＋FB'〉となるように。 ∠ABB'が60°かどうか判らないので・・・・ > (01)_四角形ABCDの頂点Aが在る側に、垂線BB'を'底辺とする〈正三角形ABB'〉を作る。 これは作れないのでは？ |
| … |
>No.101575 >ADで折り返すと、正三角形＋正五角形ができるという（実際できる）けど、 >それらが「正」三角形と「正」五角形である証明を誰かしてくれ・・・・ 回答２が言わんとする解き方は、No.101588やNo.101606で説かれてるように 〈与えられた四角形ABCD 〉≡〈辺を等しくする正三角形と正五角形とを接ぎ合わせた六角形が その最長の対角線で折半されて出きる四角形〉(**) という洞察に拠っているので、『〈与えられた四角形ABCD 〉から「正三角形＋正五角形ができる」』という事の証明を要しない。 けれども、その事については つぎのような直接推理による「論証」ができる： ¬◇［〈正三角形と正五角形の接合図形を ソレが有つ最長の対角線で折り綴じる 〉という操作で以って 〈与えられた四角形ABCDと合同(または相似)の図形 〉が作られない］ それゆえ、 □［〈与えられた四角形ABCDを ソレが有つ最長の辺で折り返す〉という逆の操作で以って〈正三角形と正五角形の接合図形〉が作られる］(***) |
| … |
(*) このさい〈作られる五角形BCDC'B'∈正五角形〉である事は この問題の“設定”に由来する。 この解き方にあっては〈作られる五角形BCDC'B'∈辺ADについて線対称な多角形〉である事の方が肝要。 (**) "≡"でなく"∽"かもしれない。 (***) "¬◇［α］"は《αという事象は不可能だ》を、"□［β］"は《βという事象は必然だ》を意義する記法。 |
| … |
>>101631-101632 よくわかんないけど、要するに「かの閃き」が必須ということですよね？ あと、101630は追加訂正。 ∠ABB'が60°かどうか以前に、AB=BB'かどうかも不明ですよね？ |
| … |
> (01)_四角形ABCDの頂点Aが在る側に、垂線BB'を'底辺とする〈正三角形ABB'〉を作る。 > これは作れないのでは？ >∠ABB'が60°かどうか判らないので・・・・ >∠ABB'が60°かどうか以前に、AB=BB'かどうかも不明ですよね？ (01)を詳しく説くと「垂線BB'を半径とし垂線の両端点B,B'を支点した２つの弧を描いて交点Aを取り〈正三角形ABB'〉を作る 」となる。 だから「∠ABB'が60°かどうか判らない」ような状況の下でも「∠ABB'＝60°」は保証される。 加えて言えば、(01)で作る〈三角形ABB'〉は〈その垂線AFが辺ADと重なる二等辺三角形〉であれば可く、〈正三角形〉であるのを要しない。 だから、「AB＝BB'」や「AB≠BB'」のどちらあってもかまわない。 ただ、与えられた四角形ABCDにあってはコレが有つ性質に因って「AB＝BB'」の方であらざるをえない。 |
| … |
描いて測ってみたら結果的に正三角形だったラッキー、では証明じゃないよ。 |