>台形の話は解りません。
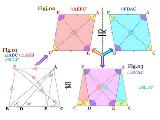
>台形の解説が聞きたい・・・・・>等脚台形は何処いった・・・・〈等脚台形についての解説〉はココ:Fig.01のようにして〈△FCBを含む△AFB+△ABC〉を作れば、いきおい「求める∠Bの角度は∠Cの角度の半分だ」という直観のデモンストレーション〈Figj.02⇔Fig.03〉が脳内でアニメ化される。Fig.01が〈Eを支点にしてAまで円弧を描いたモノ〉であればヨリ短かくアニメ化されるだろう。
数学@ふたば保管庫 [戻る]
|
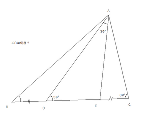
ACと同じ長さの二等辺三角形が3個ぐらいできる あとはゆっくりやったらええ |
|
BEとDCの長さに注目すべし その長さは同じか、違うのか |
|
△ABCが等脚台形となるように補助線を引き、ソレの対角線の両方を得てみよう。すると、∠Cと∠Bとの関係が顕わになる。 |
|
あー。 立ってる二等辺三角形と、右に寝てる二等辺三角形と、ずらした……か。ありがとう。 問題が解けるとだいたいスッキリするもんだけど、この手のは 「なんで気づけんか、さっきの俺!」とガッカリ感が強いわ。 いまちょっと涙目。 台形の話は解りません。 |
|
算数オリンピックの過去問だと思う |
|
台形の解説が聞きたい・・・・・ |
|
∠AECと∠ACEは? AEとACは? ∠CDAと∠CADは? DCとACは? BEとDCは? 以上から、BEとAEは? そして∠BEAは何度? |
|
等脚台形は何処いった・・・・ |
|
1分でできたおー 40°でしょう BE=AEになるからね〜 |
|
こういうのの角度三分割問題は見た事あるけど これみたいな長さ三分割は初めて見た |
|
> 「求める∠Bの角度は∠Cの角度の半分だ」という直観のデモンストレーション〈Figj.02⇔Fig.03〉が > 脳内でアニメ化される。 それって、たまたま菱形だったからでは? |
|
BF=BEをどっかで示さないとただの直感だね |