わかりやすくお願いし - 数学＠ふたば保管庫

数学＠ふたば保管庫 [戻る]

わかりやすくお願いします。
どう足掻いても解けません。
いろんな板で馬鹿にされてここにたどり着きました削除された記事が4件あります.見る

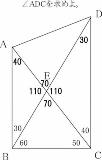
BCの長さを1とすると、DC=√3、AB=tan50°、DC-AB=√3-tan50°
∠ADC=atan(1/(√3-tan50°))≒61.617708°
illustratorで作図すると約61.6°なので概ね合ってると思われる

ニュース表でも見た
どうして最初からここ（数学板）にこないのか

内角の総和で出せるとか、補助線引いて出せるとか聞いていたので、それに固執していました…
ありがとうございました。ﾓﾔﾓﾔが晴れました

ラングレーの問題　で検索

ラングレーで検索しましたけど、二等辺三角形がないので上手く使えませんでした

これ無理。俺は解けなかった。

無理っていうのは、この問題補助線を仮定しなければならないけど、そもそも、その仮定はどこから探せばいいという意味

>BCの長さを1とすると、DC=√3、AB=tan50°、DC-AB=√3-tan50°
>∠ADC=atan(1/(√3-tan50°))≒61.617708°
うーん話聞いても全く分からん

補助線とかtanとか使わずに求められんのかな

補助線要るならそう書くべき
問題が間違っているな

自分が解けない問題は間違っているで一蹴ｗ

サクッと解ける奴いないんか（他力本願）

https://m.youtube.com/watch?v=cGcnXTwj5es

最初のレスで解かれてるじゃないか。

最初のは近似値だから嫌なんじゃ？

≒の左は近似値じゃないと思うが

「～をもとめよ」とは式を最も簡単な状態にすること。
三角関数や逆三角関数は単純計算では求めることができないので、もっと簡単な式があるやもしれず。

> うーん話聞いても全く分からん
中学レベルでがんばってみた。アーク何とか、なんてのは習った記憶がないけど表計算にぶち込めばすぐ答えが出るから便利。

DC上に点Oを∠OBC=30°になるようにおく。
BO=AO=ZOで、
∠AOB=60°なので、∠AOB=30°
よって∠ADC=60°

> DC上に点Oを∠OBC=30°になるようにおく。
> BO=AO=ZOで、
BO=AOを証明してください。
それからZOはどこですか。

> ∠AOB=60°なので、∠AOB=30°
60°なのか30°なのか、はっきりさせてください。

>BO=AOを証明してください。
>それからZOはどこですか。
>60°なのか30°なのか、はっきりさせてください。

ご指摘感謝、の前に、誤記だらけすみません。
---
DC上に点Oを∠OBC=30°になるようにおく。
BO=AO=DO、∠AOB=60°なので、∠ADB=30°
よって∠ADC=60°
と書きたかったんです。で、
>BO=AOを証明してください。
・・・orz。
私の妄想でした。ごめんなさい。
改めてご指摘感謝。

現代数学 2016年02月号に一般的なラングレーの問題の解法が載っているようだ。

超アクロバット的な手法の補助線を引いているそうだが…果たして。

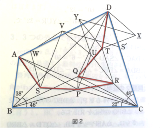本文無し

同じ正方形が傾いて、辺どうしが為す角を求める、ってのは解けなかった。
灘の入試問題。

書き込みをした人によって削除されました

坂道に強いひとならわかるかもしれない

中点、延長線から61.62°
ていうか　これ　イジワル設問だろ

そもそもラングレー問題じゃないしな。

ラングレー問題から発展した、整角四角形の問題とでも言えば良いのか？