数学@ふたば保管庫 [戻る]
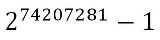
|
さあ素数を数える作業に戻るんだ スレ画の次の素数は何だ? |
|
これまでで最大の素数といっても その中間にある素数も見つけないと意味ないしな |
|
2のn乗から1を引いた数は素数になる? |
|
去年9月に見つかっていたのを気付いたのが年明けだったそうで |
|
>その中間にある素数も見つけないと意味ないしな いやいや、巨大素数は暗号強度の向上に使えるから 単発でもそれだけで価値があるんですよ |
|
そんで報奨が出るのよな |
|
これもリーマン予想を満たすの? |
|
2のn乗-1 の素数はそれ以外の素数と何か違う性質でもあるのか? |
|
ニュースになるような有名な素数じゃ暗号に使えないんじゃないのかな? 真っ先にそれ使って割ってみるだろうし |
|
>2のn乗から1を引いた数は素数になる? ならないものもある。 例えば、n=6のとき-1+2^6=63だから素数でない。 |
|
2^74207280-1や2^74207282-1は素数じゃ無いってことなんだろうか |
|
メルセンヌ素数って何でしたっけ、 |
|
メルセンヌな素数ですん |
|
>メルセンヌな素数ですん その答えは不親切過ぎる 素な数をメることはセンぬですん |
|
くらえ、必殺、メルセンヌツイスター! |
|
2は素数なので、2の倍数(偶数)は全て 2のベキ級数で展開できるから素数じゃないのだが じゃあその2のベキに±1してやったら 少なくとも2のベキでは展開できない数になるから、 因数が巨大になりやすい⇒因数が「素因数」になりやすいじゃね? という素朴な発想で、双子素数とかメルセンヌ数とか探してるんだよ 実際、そうやって見つけてるしね |
|
そういやそうでした(てへぺろ |
|
2^(mn)-1 = (2^m-1)(2^m(n-1)+2^m(n-2)+...+2^m+1) だから2の肩に載ってる数は素数に限られる ってことで巨大素数を発見しやすいのでは? 同じ発想でa^p-1の形の素数も特別視されたりするんだろうか |
|
>a^p-1 aを2以外の素数とする限りテラ偶数やん? |
|
2*n-1 これじゃダメなの? |
|
2より大きい素数は奇数なのだからそれでも問題ない。ただ、調査量は少なくて済む。 |