数学＠ふたば保管庫 [戻る]
|
歩く方がたくさん濡れます 違うと思う人は歩けば宜し |
|
昔テレビでやってた実験では、どちらも大して変わらない。 歩けば頭と肩が濡れる。 走れば正面全体と、ふくらはぎ（水はね）が濡れる。 量よりもどこを濡らすかみたいな話だった。 |
|
もし無重力下で雨粒が動かないところを水平に直線移動すると考えたら人間の移動した部分の体積は速度に依存せず同じな訳だから得られる水滴の数は変わらない これは逆に言うと、重力下で無限の速度で移動した場合に相当する 次にその移動を斜め上に移動すると考える。これは雨粒が下に直線移動しているのとほぼ同じ。これは、ある実時間を持って移動した場合に相当する ちなみに止まっている場合、垂直に移動しているのと変わらない つまり |
|
書き込みをした人によって削除されました |
|
単位時間あたりの濡れ量は、 空中の雨滴の密度ρと落下速度v_vが一定だとして 人物の歩行速度v_hと人物の立体形状で決まる v_vとv_hの合成ベクトルvの向きに見込んだ 人物の投影面積×|v|が最大になるv_hのとき、 単位時間あたりの濡れ量が最大となる これが単位時間あたりの濡れ量を問題にしているのではなくて、 学校から家に帰り着くまでの総濡れ量とかだともっと複雑になる |
|
その場に止まって動かないのが濡れ量最大ではないか |
|
針(ただし断面積0)のように細い人が雨滴の落下方向と平行に突っ立ってるんだったら？ |
|
雨粒の大きさがあるからいつか当たる |
|
ｽﾏﾝ断面積0ではまずかったorz 改めまして、直径20 cmで身長3000 kmの円柱状の人物だったら？ 簡単のために雨粒の落下速度を1 m/秒とすると、 1時間突っ立っても濡れ量は π×(0.1 m)^2 ×ρ×3600 秒×1 m/秒 = (36π m^3)×ρ だが、10秒で1 m 水平移動したらたちまち 0.2 m × 3000×1000 m × 1 m ×ρ = (600000 m^3)×ρ に多少増しぐらい濡れる（増し分は、10秒のうちに降ってくる雨粒の分 ここでρは雨粒の空中密度 |
|
>No.79385 整理してから書け ここはオマエのメモ帳じゃねーぞ |
|
ランダムに上から粒が降ってくるプログラムでも作って歩くのと走らせるのでどっちが多くヒットするかカウントしてみれば？ |
|
>ここはオマエのメモ帳じゃねーぞ 俺はそのメモ帳を最大限の興味を持って見ている。 邪魔しないでくれないか？ 久しぶりに数学板らしい見解が重なりつつあるんだから。 |
|
雨を停止と考えてXY-t座標で 表面積がはく面積積分したら？ |
|
>数学板らしい見解が重なりつつあるんだから。 で？ 結論は？ ぐだぐだ間違いを書き連ねるのを見解だと思ってる馬鹿に訊いても仕方ないけど一応な |
|
むかし、教育放送での実験では 走る方が歩くより濡れかたが少なかった |
|
単位時間あたりの濡れ量最大化条件については No.97872で結論を出しているわけだが… 藻前さんがしばしば言う「整理してから書け」は ほとんどの場合意味がわからんね… |
|
これは前に話題になってた（ここじゃないが）。 結論は走った方が濡れない。 http://iopscience.iop.org/article/10.1088/0143-0807/33/5/1321/meta http://www.bbc.com/news/science-environment-18901072 |
|
>No.97872で結論を出しているわけだが… そう思いこんでるのは君とNo.97882だけじゃないかな |
|
>No.97872で結論を出しているわけだが… 結論というのは 最低でも「どちらが濡れる量が少ない」くらいは書かないと認められないね 「時速○ｋｍが一番濡れる量が少ない」ってのが結論だろ |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
>No.97894 スレ題には人物の立体形状が規定されていないから No.97872までしか言えないのである 常識的な立体なら、時間当たりの濡れ量はv_hに対して単調増加する （歩行速度が速いほど一定時間内に人体にたくさんの雨粒に当たる とは言えるがそれぐらいNo.97872から演繹して欲しい、 ただ、厚さ0の絨毯みたいな人物だったとしたら速度によらず 時間当たりの濡れ量一定になるのもNo.97872から明らかなので 数値を問う向きには人物の立体形状を規定する義務がある、 |
|
書き込みをした人によって削除されました |
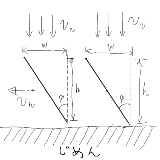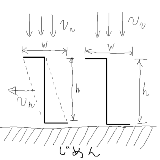
 人物の立体形状依存で、静止しているよりも歩いた方が 単位時間あたりの濡れ量が減少することもあるという病的な反例貼る、画像は人物の側面図で、奥行きはZとすると、静止したときは単位時間あたりの濡れ量はW*Z*v_v一方、図の水平な矢印の方向に、ある速度v_h（ただしv_v*(H/W)以下）で移動すると、単位時間あたりの濡れ量は (W*Z*cos(θ)*√(v_v^2 + v_h^2)となり、W*Z*v_vより小さい濡れ量を示すv_hが存在する、ここでθ=arctan(v_h/v_v)v_hの値は解析的には漏れには計算できんorz |
|
書き込みをした人によって削除されました |
 ていうかさらに病的なの貼る、 画像の側面図のような厚さ0の平面状の人物だったとして、奥行きはZとして、静止したときの時間当たりの濡れ量はW*Z*v_vだが、画像の水平方向矢印の方向に速度 v_h = v_v * sinφで移動したならば、全く濡れずに住む（v_vとv_hの合成ベクトルvの大きさ|v|が濡れ量の式に現れず、 かつv方向から見込む人物の投影面積が0ここでφは鉛直方向に対する人体の傾き（厳密にはベクトルv_vとv_hが張る平面上で図る角度だから雨が降ったら進行方向に向かって傾いた厚さ0の平面になれば良い |
|
またやってるのかコイツ 自己顕示欲が強いヤツだ そのうち犯罪犯してニュースに出るね |
|
屁理屈大好き人間が集まる掲示板って 結局こうなるんだな・・・ |
|
それは発題者が必要だった物なのか あと地球の重力が大きく変化する事を考慮していない |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
>No.97907 >それは発題者が必要だった物なのか No.97872の計算モデルこそ、 >走れば地面に落ちる前の雨粒をたくさん体が拾ってしまうと思うんだ。 というスレ主の観察の定式化なわけだが… で、少なくとも、このスレで挙げた個別の立体例についてなら、 濡れ量最小値になる移動速度v_hの存在とか、全く濡れないとかいったことがらを証明できるから、 誤りの可能性は小さいと見る（検証が必要だが結論はNo.97869やNo.97892にも一応符合する >あと地球の重力が大きく変化する事を考慮していない そんなのは雨粒の速度v_vに分布（確率密度関数）を考えて、 No.97872のモデルに基づく濡れ量の関数との積をv_vについて積分すれば良いのでは… 現実の雨粒が鉛直に降らない件（方向がばらばら）も同様に処理し得る んで、No.97905の考える屁理屈じゃない理屈というのがあるならお伺いしてみたい希ガス |
|
>んで、No.97905の考える屁理屈じゃない理屈というのがあるならお伺いしてみたい希ガス 結論がない理屈は全て屁理屈 つまりNo.97876以外の長文は全て屁理屈 直径20 cmで身長3000 kmの円柱状の人物の場合だが結論を出しているから評価できる |
|
>んで、No.97905の考える屁理屈じゃない理屈というのがあるならお伺いしてみたい希ガス No.97905が屁理屈じゃない理屈は無いとでも言ったのかよ？ オマエが屁理屈大好き人間だからカチンと来ただけだろ 逆切れして八つ当たりすんな |
|
普段の実生活でわかることだろ…… |
|
ごちゃごちゃごちゃごちゃ言ってっけどさ No.79385さんは結局どっちがどれくらい濡れないかをさっさと書きなよ |
|
何言ってるの、濡れ濡れよ |
|
||￣￣￣￣￣￣￣￣￣￣|| || あらしは ｡ ∧_∧ いいですね。 || 無視！ ＼ (ﾟーﾟ*) ||＿＿＿＿＿＿＿＿⊂⊂ | ∧ ∧ ∧ ∧ ∧ ∧ |￣￣￣￣| ( ∧ ∧ ( ∧ ∧ ( ∧ ∧ | | 〜（＿( ∧ ∧ __( ∧ ∧__( ∧ ∧￣￣￣ 〜（＿( ∧ ∧＿( ∧ ∧＿( ∧ ∧ は〜い、先生。 〜（＿( ,,)〜（＿( ,,)〜（＿( ,,) 〜（＿__ﾉ 〜（＿__ﾉ 〜（＿__ﾉ |
|
>No.97903 消防の時分に放課後の教室で黒板にベクトル図を画いてアレコレ言い合ったのを思い出したよ(遠い目 やっぱり前傾板状人間を想定していた ガキだったから雨の落下速度や当った雨粒の時間的総量までは考慮出来なかったな 濡れるのが一番少ない速度が存在し、それより速くても遅くても濡れ方が増大するのではないか、というのが確か当時の結論だった でも「私は走ると転ぶから絶対走らない！」という横からの発言にはその場の全員が納得したっけ いやーなっつかしーなー・・・ |
|
>でも「私は走ると転ぶから絶対走らない！」という横からの発言にはその場の全員が納得したっけ 俺は雨がふっている中には出ていかない |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
||￣￣￣￣￣￣￣￣￣￣|| ||No.97945は ｡ ∧_∧ いいですね。 || 荒らし！ ＼ (ﾟーﾟ*) ||＿＿＿＿＿＿＿＿⊂⊂ | ∧ ∧ ∧ ∧ ∧ ∧ |￣￣￣￣| ( ∧ ∧ ( ∧ ∧ ( ∧ ∧ | | 〜（＿( ∧ ∧ __( ∧ ∧__( ∧ ∧￣￣￣ 〜（＿( ∧ ∧＿( ∧ ∧＿( ∧ ∧ は〜い、先生。 〜（＿( ,,)〜（＿( ,,)〜（＿( ,,) 〜（＿__ﾉ 〜（＿__ﾉ 〜（＿__ﾉ |
|
物体が速度(v,0,0)で運動し、雨が一様に速度(u_x,u_y,-u_z)、地面に単位面積単位時間当たりの降水量ρで降っている場合を考える。 物体から見た雨の速度↑v'=(u_x-v,u_y,-u_z) ↑v'に直交する平面への物体の射影の面積をS_1(↑v')とする。さらにこの射影を地面に射影しその面積をS_2(↑v')とする。 さてS_1,S_2と任意の側面で囲まれる立体を考えると、この内部に水が溜まることはないので、S_1とS_2を通過する雨量は常に等しい(側面は常にキャンセルするので通過雨量=0)。また地面への降水量ρは空間中の雨の密度と下向きの速度u_zのみで決まるため物体から見た系でρは変化しない。 以上から単位時間当たりに物体が浴びる水量VはV=ρS_2(↑v')となる。 |
|
ごめん、S_2のとりかたが間違ってた S＿2は地面上にあってS_1の面に射影するとS_1に一致するように取らないと側面の通過雨量が0にならない |
|
上で話題に上がっている一番濡れない速度だけど 単位長さ移動する際に物体が浴びる水量ρS_2(↑v')/vを最小にするようなvを求めればいいんだと思うよ 機械的な計算でできるから適当に物体の形決めて誰か暇なやつ計算してみてくれ |
|
>誰か暇なやつ計算してみてくれ 結局これかよｗ |
|
>結局これかよ はぁ？公式的な式まで挙げてやったんだから気になるなら自分でやれよカス |
|
人間の形状を奥行きがd,高さがhの長方形で近似 家までの距離をl,雨の速度をu,歩行速度をvとすると濡れる量は hl+dlu/vに比例 前面が濡れる量は歩行速度によらない 上面が濡れる量はv→∞で0 |
|
>公式的な式まで挙げてやったんだから気になるなら自分でやれよカス 最後までやり遂げる事が出来ないカスが泣き叫んでるｗｗｗｗ |
|
No.98013はそんなに忙しいのか？ 暇がないなんて馬鹿が言う事なんだが |
|
何もやってない奴らに言われてもって感じなんだが 時間はあるけど考えるの面倒だよね、やればできる自信はあるけど |
|
何もやってない No.98027が言うなって感じなんだが 考える時間はあるけど結果を出す能力が無いんだろ やれない癖に自己主張だけは一人前ってカスの典型だな |
|
No.97986，No.97987にある計算の基礎となる公式の導出が何もやってないことになるのかよ No.97990が理解できれば物体の形状決めてρS_2(↑v')/vが最少になる条件で計算してしまえば局所的にはそれで終わりなんだが そんな単純計算は自分でやれ、俺はこの公式まで出した時点でこの問題は終わってんの |
|
>計算の基礎となる公式の導出が何もやってないことになるのかよ 答えを出さなかったら終わってないと思うのが常識だバーカ >局所的にはそれで終わりなんだが 勝手に局所的にすんなよアホー >そんな単純計算は自分でやれ オマエがやれやカス >俺はこの公式まで出した時点でこの問題は終わってんの オマエ自身が終わってんだよクズ |
|
>やればできる自信はあるけど ははは おならプ〜 |
|
雪がしんしんと降る時にふと思い出す問題 そっと回避しながら前に進む |
|
>俺はこの公式まで出した時点でこの問題は終わってんの 終わってるのは問題じゃなくオマエの人生だろ 詰んでるとも言うｗ |
|
>答えを出さなかったら終わってないと思うのが常識だバーカ それは技術屋の世界の常識かもしれん。 でも数学屋の世界じゃ常識ではないな。むしろ非常識というか、変わり者というか、本質を理解してないって疑われるかも。 |
|
>でも数学屋の世界じゃ常識ではないな。むしろ非常識というか、変わり者というか、本質を理解してないって疑われるかも。 出せる答えを出さなかったら終わってないと思うのが常識だと思う 君に本質を語る資格は無いね |
|
>それは技術屋の世界の常識かもしれん。 いいえ世界の常識です ごく少数の阿呆が勝手に自分だけの常識を設定して数学屋を騙っているだけです |
|
抽象的な理論と具体的な結果のどちらに重心を置くかは個人の思想によるんであって他人がとやかく言うことじゃないでしょ |
|
>勝手に局所的にすんなよアホー 以下雨の空間的、時間的変動が物体の大きさに比べて小さい場合を考える(条件を課すのは変化が物体に対して小さければ各時刻で局所的に一様な雨とみなして前述の公式が適用できるから) 時刻t,位置r↑=(x,y)における雨の速度(u_x(x,y,t),u_y(x,y,t),-u_z(x,y,t)),単位時間単位面積当たりの降雨量ρ(x,y,t)とする。 r↑(t_0)=r_0↑からr↑(t_1)=r_1↑まで経路γ=(x(t),y(t))にそって移動する際に濡れる量Z[γ]は Z[γ]=∫_γ dt ρ(x,y,t)S_2(u_x-v_x,u_y-v_y,-u_z) Zを最小にするような経路が満たすべき方程式はオイラーラグランジュ方程式より ∂(ρS_2)/∂v_i=d/dt (∂(ρS_2)/∂x_i), [i=1,2,v_1=v_x,v_2=v_y] この偏微分方程式を解けば大域的な性質を反映できるわけだけど物体の形状によって直線か回り込むかが変化する場合とか構成できると面白そう |
|
>抽象的な理論と具体的な結果のどちらに重心を置くかは個人の思想によるんであって いいや違うよ 質問者の思惑によるんだよ 本気で書いてる？ 馬鹿にしちゃうよ？ |
|
>いいや違うよ >質問者の思惑によるんだよ 教師-生徒の立場での質問だったらその通りだと思うよ 別に質問に答える義務があるわけでもないし誰かが強制する権利も無いだろ、ここ掲示板だし |
|
>教師-生徒の立場での質問だったらその通りだと思うよ じゃあここは教師-生徒の立場での質問じゃないんだから君の指摘はあたらないよね >別に質問に答える義務があるわけでもないし誰かが強制する権利も無いだろ、ここ掲示板だし 義務とか権利を言いだしちゃったよｗ じゃあ私が君と違う方に重心を置いていても君に強制される謂れは無いだろ、ここ掲示板だし |
|
重心を置くとかの屁理屈は要らないので 質問に答えたい人だけがレスをすれば いいと思う 常識についても論争ウザい |
|
質問者の思想に合わせるべきだというから 質問者と回答者のどちらの思想に合わせるか(もしくは合わせる必要がそもそも無い)は関係性で変わるだろうと指摘したつもりなんだが伝わらなかったな |
|
>関係性で変わるだろうと指摘したつもりなんだが伝わらなかったな 関係性ってなんだ？ 正直ナニ言ってっか全然伝わらないね 自分でもよく解らないで言ってっだろおまえ |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
>質問者と回答者のどちらの思想に合わせるか(もしくは合わせる必要がそもそも無い)は関係性で変わるだろうと指摘したつもりなんだが伝わらなかったな いや、充分に伝わったよ 君が我儘で独り善がりだと言う事は |
|
ここまでオイラーラグランジュ方程式が間違ってる指摘無し |
|
いま 修羅の国がこの状態w |
|
スレ主は間違ってる 例えば、雨を流率を持った川の流れと仮定してみる、 そこに[無限吸収体]か[発電媒体]とかのβ体を考える、 無限に速く移動すれば… 水分子の隙間を高速で避けて移動すれば 『濡れない』、 って言うのは置いといて、 移動速度が遅いほど水分子の流れを受けるよね？ つまり 速く移動した方が濡れ具合が少なくなる |
|
>質問者と回答者のどちらの思想に合わせるか そりゃ質問者だろ 回答者だと思ってる奴は半島出身だろ |