数学@ふたば保管庫 [戻る]
|
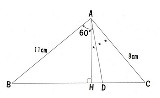
垂線の長さから星の角度を決める式を作る 11cos(π/3-☆)=9cos(3☆) 題意の角度☆=2arctan((3√3-2√5)/7) 一方求める長さの比は☆を代入して計算すれば 11sin(π/3-☆)/(9sin(3☆))=11/7 カッコ悪い回答だけど答えが綺麗な形してるから幾何的に解けるんだろうか |
|
回答は答えを見たら正解です。スレ主(というほど エラそうには言えませんが)としてはお言葉通り 幾何的に答えが出てほしいなあ、と・・・ (でも数学オリンピックの問題とのことなので、 三角法は使わないとダメなのかもしれませんが・・) |
|
97284さんの答えから逆算して考えましたが 線分AB上にAP=9cmとなる点Pを、直線AD上にAQ=9cmとなる点Qを点Dの外側に取る。 また線分BH上にC’H=CHとなる点C’を取る。 このとき点P, C’, Q, Cは点Aを中心とする半径9cmの円の円周上にある。 ∠HAD=θとすると、∠C’PQ=(1/2)*∠C’AQ=2θ、△APQは正三角形なので∠APQ=60°、 ゆえに∠APC’=2θ+60°…(1) また、△APC’は二等辺三角形なので∠AC’P=2θ+60°、∠AC’H=90°-3θより、∠PC’B=θ+30°…(2) (1), (2)より、∠PBC’=θ+30° よって△PBC’は二等辺三角形である。 ここで直角三角形ABHの斜辺ABの中点Mを取ると、△MBHは△PBC’と相似な二等辺三角形なので、 BH:CH=BH:C’H=BM:PM=11:7 |
|
ABHをABを軸に折り返す(新しく出来る点をH') ABH'をAH'を軸に折り返す(新しく出来る点をB') するとCAB'は一直線上((60-★)*3+3*★=180より) AB'=11 あとは角の二等分線と面積比で |
|
なるほどその発想はなかった |