数学@ふたば保管庫 [戻る]
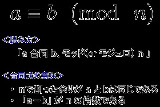
|
合同式の場合、nを数回足しても引いても結果は同じ だからaの代わりにa+nでもOK |
|
この場合2乗でまとめればa^2>nになるから それで頑張って計算できるでしょ |
|
>この場合2乗でまとめればa^2>nになるから >それで頑張って計算できるでしょ 562^2=315844 315844≡140 (mod589)までは進めることが出来たんだけどこっからどうすればいいのかがお恥ずかしながらイマイチ理解出来ていない 589*140 mod 589 を求めて出た答えにまたaをかけると最終的にa^13 mod bにはなるんだけど合同式の性質をどう使っているかも理解が怪しい |
|
いわゆるロシア農民法の応用で a^2 = a × a a^4 = a^2 × a^2 a^8 = a^4 × a^4 a^13 = a^8 × a^4 × a と計算すれば手間が少ないよ |
|
>と計算すれば手間が少ないよ http://isw3.naist.jp/~kaji/lecture/10/inf-theory/13-4up.pdf これのp16で似たようなことやっててとりあえず目的の値を出せたは良いものの何故 >12^2mod35=144mod35=4 >14^4mod35=4^2mod35=16 になるのかが理解できないっぽい (14^4)≡(4^2)mod35が成り立つってこと? |
|
12^4mod35=4^2mod35=16 の誤記ではないですか? 一般に、A≡a, B≡b (mod n)のとき A × B ≡ a × b (mod n) が成り立つので 12^2 ≡ 4 (mod 35)より 12^4 ≡ (12^2) × (12^2) ≡ 4 × 4 ≡ 16 (mod 35) が成り立ちます。 |
|
書き込みをした人によって削除されました |
|
modの定義知ってるなら >(14^4)≡(4^2)mod35 が成り立つかどうかぐらい考えればわかるでしょ 14^4=(35*4+4)^2 =(35*4)^2+2*4*35*4+4^2 =35*(35*4*4+2*4*4)+4^2 |