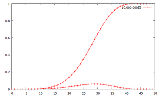
シミュレーションの結果27.7回になった
真面目な数え上げプログラムは面倒だからやらない画像はn回目にビンゴする確率分布と積算分布
数学@ふたば保管庫 [戻る]

|
問題を出すだけであとは投げっ放しが多過ぎる あとどうやって正解を示すんだ?そこまで考えて問題を出してくれよ |
|
n=選ばれた番号だとしたら リーチの時のあたり確率は1/(50-n)だとしても リーチになる確率を求めるのは結構面倒だな |
|
「ビンゴ 平均」で検索
23回前後らしい。 |
|
書き込みをした人によって削除されました |
 シミュレーションの結果27.7回になった 真面目な数え上げプログラムは面倒だからやらない画像はn回目にビンゴする確率分布と積算分布 |
|
こういうのってざっくりでも簡単な求め方がわかると便利だよな |
|
実際に並べてみると 100%ビンゴさせるには最長で18か所に印をつける必要があるんだけど 印の付かない読み上げが26ヶ所あるから最長で43回まで外れる計算になる だけどこんなのは極めて低確率 可能な限りリーチを避けても 13ヶ所目では必ずリーチになるので むしろこのあたりで当たりを避け続けるほうがむずかしくなってくる 読み上げる数字が全部で50なら確率1/2で何かしら印が付くから2倍して26箇所くらいと考えると やっぱり上のシミュレーション結果みたいになるんだろうな |
|
100%ビンゴなら最多で20か所に印をつける必要があるんじゃないかな 19箇所埋めてもビンゴならない組み合わせがあって 4つの□だと横1列,縦1列のビンゴを絶対に止められないから □■■■■ ■■■□■ ■□★■■ ■■□■■ ■■■■□ |
|
可能な限りリーチを避けたら 15回目で必ずリーチになるが正しい 適当なこと書きすぎ ■■■□□ ■□□■■ □■★■□ ■■□□■ □□■■■ |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
書き込みをした人によって削除されました |
|
ルールがよくわからんorz ゲーム開始時点でプレイヤーはそれぞれ4個の数からなる縦、横、斜めx2の4数列 (4数列を通して項の数の重複無し)を持っており、 (スレ画だと(3,13,31,47),(49,32,11,8),(9,19,33,44),(29,26,23,28)の4数列 それらから司会者が読み上げる1〜50の範囲内の数(重複無し)を消しこんでいったときに、 4数列のうちどれかにおいて、数列全体が完全に消し込まれたところでBINGOってことでおk? BINGO条件が仮に1数列の消しこみと仮定したとき、読み上げ個数nに対して数がヒットする確率は 1-{(1-(4/(51-n_1))^(n_1)} (残り4個中のどれかがヒットする、ゲーム開始状況に対する事後確率) 1-{(1-(3/(51-n_2))^(n_2-n_1)} (残り3個中のどれかがヒットする、上の事象生起に対する事後確率) 1-{(1-(2/(51-n_3))^(n_3-n_2)} (残り2個中のどれかがヒットする、上の事象生起に対する事後確率) 1-{(1-(1/(51-n_4))^(n_4-n_3)} (残り1個中のどれかがヒットする、上の事象生起に対する事後確率) |
|
書き込みをした人によって削除されました |
|
ここで、n_1, n_2, n_3, n_4は、 残り個数がそれぞれ4, 3, 2, 1個の状況でヒットした場合の読み上げ個数nで、 これらは1≦n_1<n_2<n_3<n_4≦50を満たす任意の組み合わせを取り得る。 ので、1数列の消しこみが読み上げ個数nで終わる確率Pr(1, n)のは、 Pr(1, n) = Π[0≦n_1<n_2<n_3<n_4≦n](上述4式の積) よって、4数列のどれかがBINGOになる(本来のBINGOの)確率は Pr(4, n) = 1 - (1-Pr(1, n))^4 てことでおk nの気体値は当然 E[n] = Σ[k=1..50](k * (Pr(4, k)の確率密度関数)) = (Pr(4, n)が1/2となるn) 0≦n_1<n_2<n_3<n_4≦nの組み合わせを列挙するのが面倒に思えるので検算とか具体的数値のは略 気が向いたらPerlか何かでやる鴨、 |
|
ビンゴのルール知らないって言うのも珍しいなあ |
|
スマンNo.97188の確立の式まつがえてたorz BINGO条件が仮に1数列の消しこみと仮定したとき、読み上げ個数nに対して数がヒットする確率のそれぞれの式で n_k→(n_k-1) と置換(n_k-1個までヒットしない確率)としてた上で、 さらに(n_k個目でヒットする確率)(5-k)/(51-n_k) を掛ける必要があったわ; ここでk=1,2,3,4。 |
|
これヤフーモバゲのソリティアだね |
|
うちの学生にシミュレータを作らせて 初めてビンゴに到達するまでの回数(初到達問題) を解かせてたあのころ...13回ぐらいだったような 気がするな |