数学＠ふたば保管庫 [戻る]
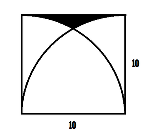
 宿題か？ ヒントやるからあとは自分で解きな |
|
線の太さが与えられてないんですが |
|
>>線の太さが与えられてないんですが キモ |
|
これモンテカルロ法で値を出すにはどうするのが早いか |
|
１００−５０π/３−２５√３ |
|
そのカラフルな図には載ってないけど 正三角形の左右に円の1/12が有る事に気づけば簡単だね。 |
|
>キモ ヒントの人くらいならともかく、スレ画は太すぎ |
|
>そのカラフルな図には載ってないけど >正三角形の左右に円の1/12が有る事に気づけば簡単だね。 それが最も簡単な解答かな？ |
|
補助線ひこうぜ |
|
ああ、なるほどね すげー簡単！ |
|
面白かった。 出題してくれた人、どうもありがとー！ |
|
ヒント画像が出たおかげで台無し それを考えるのが楽しいと思うんだよね。 |
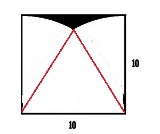 >正三角形の左右に円の1/12が有る事に気づけば簡単だね。 やっと理解できた |
 じゃあこれは？ 大阪星光学院中学の1014年度の入試問題より。しかし30度/60度/90度の直角三角形の辺の比なんて小学校で習ったっけ？ |
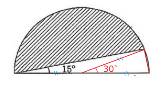 小学校問題かな？ こんな方法しか思いつかない |
|
良い問題ですねー 流石、星光学院ですね。 二等辺三角形＝１８×１８÷２÷２＝８１ 中心角３０°の扇形の面積＝１８×１８×３．１４÷１２ ＝８４．７８ 半円の面積＝１８×１８×３．１４÷２＝５０８．６８ 従って、508.68-81-84.78=３４２．９㎠ |
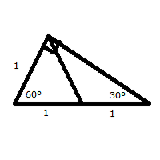 ＞30度/60度/90度の直角三角形の辺 図のように小学生の知識でも求められるけどたぶん覚えているんだろうねとはいえこの問題だともっといい解き方があるのかもしれないが |
|
小中学生レベルの面積の問題ってほんと楽しいよな |
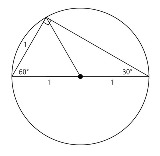 >図のように小学生の知識でも求められるけど その図で右下の長さが１になるのは自明だろうか？と思ったのですが、外接する円を描いてみたら、なるほどでした。 |
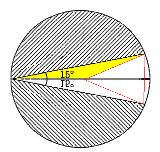 俺こう考えた。 黄色の△の面積をどうやって求めるかこの問題の面白いところだと思った。なんか図はいい加減だけど、赤い△は正三角形やね。なので、黄色の△は底辺18cm、高さ9cmの△と分かる。平成教育委員会で、黄色の△の面積を求めよ、という問題があったのを思い出した。 |
|
簡単な図形がちょっと切り取られているとか、 そういうのが多いよね |