数学＠ふたば保管庫 [戻る]
|
トップページに「プログラムで解く数学の問題集です。」 |
|
最短はd=4で例示されてるような台形の経路の内のどれかかね？ |
|
書き込みをした人によって削除されました |
|
動的計画法で何とかならないかな |
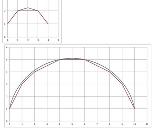
 スレ主です。久々に問題解答を再開して自分なりに 分かったので日記帳程度に書きます。①格子点の制約を無くして速さがyで与えられるようにすると最速アプローチはy=sqrt((x-xmax/2)^2+(xmax/2)^2+1)の曲線で得られる。②例題のxmax=4,10の場合についてグラフ化すると最速曲線に最もフィットするように直線頂点を格子点上で選んでいるように見えるここまで来たがxmax=1000の場合については例にしめしてある数値にならない(近い値を得ることはできた)なんかいいアルゴリズムは無いものか。 |
|
動的計画法で考える。 各格子点(x,y)ごとに、(0,1)からその格子点までの最短所要時間と経路(≒直前の格子点)を求めることを考える。 0≦x≦a-1までの各格子点の最短所要時間が既に求められているなら、x=aでの各格子点の最短所要時間を求めることが出来る。 演算時間がO(N^3)程度になるが、一応答えは出る気がする。 あとは左右対称性とか単調増加とかを使って演算量を減らせると思う。 |
|
ジャンプアクションゲームに応用できそうなできんような そんな問題だな |
|
>0≦x≦a-1までの各格子点の最短所要時間が既に求められているなら、x=aでの各格子点の最短所要時間を求めることが出来る。 これがうまくいかないんだな。 例えば、x=0～4の場合の通路を2度繰り返しても x=0～8の最短経路にはならない。 つまり、一歩前の最適解から今の最適解を出す っていう漸化式的な計算が効かないんです。 一歩踏み出した影響は最後まで影響してしまう… そこが変分とかのややこしい世界です。 |