XY直交座標上の放物 - 数学＠ふたば保管庫

数学＠ふたば保管庫 [戻る]

単純な求積問題ですが

XY直交座標上の放物線； Y = a ･ X^2　(aは正の定数) を、Y軸(鉛直軸)を中心に回転してできる放物面を内面にもつ容器があります。
内面の底からの高さが100%のところまで水を注いだとき(図中の赤色で示す部分)の内容量に対し、内面の底からの高さが80%のところまで水を注いだとき(図中の青色で示す部分)の内容量は何倍になりますか？
（図は容器内面の、XY平面による断面図)

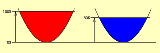
単純な求積問題ですが
単純な求積問題です

青が少ないのに何倍か聞くの？

うんとりあえずお前も帰れ

多分、相似比が５：４なので
体積比　５×５×５：４×４×４＝１２５：６４
ちゃうかな。積分すべきかな。

>多分、相似比が５：４なので

見た目で数学をやるタイプは伸びない

相似じゃないな

＞積分すべきかな
素直に機械的に積分しても、数分で計算できる簡単な問題です。

100％の時の高さが指定されてないが答えは一定値に成るのか？

答えはその変数の関数となる

>100％の時の高さが指定されてないが答えは一定値に成るのか？
とりあえず、100%の高さのY座標を b とでも置いて
計算してみて下さい。

この問題、aって要るの？