数学＠ふたば保管庫 [戻る]
|
5 12 13 |
|
84だろうか... |
|
>84だろうか... 正解 |
|
どの層で低いの？学校出てだいぶ経っている層だと ヘロンの公式を忘れているのは結構多いぞ。 |
|
9 12 15 |
|
>どの層で低いの？学校出てだいぶ経っている層だと >ヘロンの公式を忘れているのは結構多いぞ。 強者はヘロンなぞ使わん |
|
ヘロンは出番なし。 |
|
ヘロンの公式を使えという命令 |
|
14*12/2＝84 |
 ぶっちゃけピタゴラス数を知らないなんて どう考えてもゆとりだと思うのですよ。 |
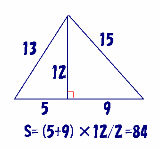 本文無し |
|
こんなの魔法使いにしか解けないよ。 |
|
えっ？ヴァージン限定？ |
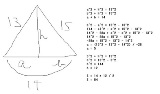 本文無し |
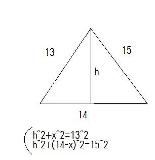 普通に連立解けば高さが出てくる |
|
三平方の定理かな。当てはめればいいんだね。なんとなくわかった。 |
|
ヘロンの公式を使えば連立方程式なんて 解かなくていいから楽だろ。 「普通に連立解けば高さが出てくる」とか ドヤって書き込むのか分からん。 |
|
１５を底辺にしてみたい |
|
１３だと底辺なことになりそう |
|
これ、1385990884456.jpgの時点でコラだろ 元の図では高さが簡単にわかる図だった 三角比から求める式は必要なかったはず |
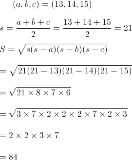 ……やっぱりあんま使いたくないな |
|
>ヘロンの公式を使えば連立方程式なんて バカ丸出し なぜお前がバカだと断言出来るのか 説明が必要かな？ あとお前は学生時代、数学の成績悪かっただろ？ |
|
>なぜお前がバカだと断言出来るのか >説明が必要かな？ 説明してくださいお願いします |
|
国語の成績の悪そうな馬鹿の説明が楽しみ |
|
>なぜお前がバカだと断言出来るのか >説明が必要かな？ いいえ 必要ありません それは説明だけでなく 貴方の存在も |
|
「数学＠ふたば」って 数学好きな気になっているだけの元コンプレックス患者が数人いるような気がするんですが、どうでしょう？ |
|
元コンプレックス患者ってなんですか？ |
|
ここまで余弦定理は出てこないが |
|
5+9＝14に気づけばあとはピタゴラス数を当てはめて…。 まぁ、ヘロン公式以前に暗算でも解けてしまうな。 二次式の因数分解でなんでもかんでも解の公式を使うようなもんで、この問題にヘロンの公式は要領がよくないな。 暗記と計算の腕力（といってもこの問題では大したことはないが）に自信があるなら解き方は間違ってないから、ヘロンの公式でもいいが。 |
|
>二次式の因数分解でなんでもかんでも解の公式を使うようなもんで、この問題にヘロンの公式は要領がよくないな。 システムに実装するなら解法アルゴリズムをできるだけ減らした方が開発効率がいいので 一概に「この問題にヘロンの公式は要領がよくない」とは言えないのでは？ |
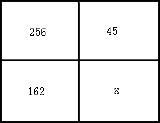 xの面積は？ |
|
162*45/256 |
|
酷い「問題らしきもの」だな。 書いてある数字は番地か？ |
|
>システムに実装するなら解法アルゴリズムをできるだけ減らした方が開発効率がいいので その場合はその通りだな。 それでも大した違いはないが。 |
|
>システムに実装するなら解法アルゴリズムをできるだけ減らした方が開発効率がいいので そもそも問題の回答条件を取り巻く普遍集合を定義していないからな。 スレ画のお題に沿った解釈として、筆記問題としてみた解釈としてはヘロンの公式を使うまでもないという意味だよ。 別に使いたければ使ってもいい。 まぁ、補助線で直角三角形二つに分ける考え方も、ヘロンの公式自体を導き出す方法の一つそのものと同じやり方だしね。(他にも方法はある） |
|
以前、ドカタのアルバイトをしていたことがあるけど みんなヘロンだけは知っていた。 高校しか出ていないような人らだけど。 道路のアスファルト工事でも、全部三角形に分割して面積を出すんだ。 なんの計算をやってるのかは理解せずにブラックボックス的に とりあえず距離さえ測れば面積になる（金額になる）って考えだった。 |
|
それはそれで否定はしないよ。 公式覚えて問題を解くというのも一つの手だ。 もともと測量の為に考え出されたものだろうしね。 |
|
1386420769917.png おもしろｗｗｗ 単位ねえ（ネタ） |
どっかで見た問題
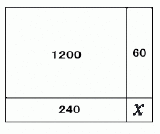 四角形はすべて長方形であるとする。 数値はそれを囲っている長方形の面積である。Xの面積を求めなさい。 |
|
書き込みをした人によって削除されました |
 ぶっちゃけ、 (a+b) は a の m 倍の面積 且つ b の n 倍の面積 と置くと、 (c+d) は c の m 倍の面積 且つ d の n 倍の面積 となるので、a：c = ma：mc = (a+b)：(c+d) = nb：nd = b：d∴ a：c = b：d題意より、a = 1200 、b = 60 、c = 240 、d = x であるから1200：240 = 60：x∴ x = 12なのですよ。 |
|
>∴ a：c = b：d これってこねくり回さなくてもいきなり出てくるんじゃないの？ |
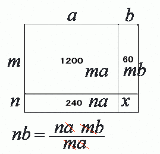 だよな |
|
ロリ二次画像が無いから、 ニセぶっちゃけ師じゃねーの。 |
|
横の比率 20:1 縦の比率 5:1 2400*1/20*1/5=24 |
|
はっ？2400じゃなくて1200じゃぞ 1200*(1/20)*(1/5)=12 |
|
>横の比率 20:1 >縦の比率 5:1 > >2400*1/20*1/5=24 定数間違い以前に、なんでわざわざ要らん計算増やすんだよぅ 240/20=12 か 60/5=12 でいいじゃないか |
|
リニアな軸とはかぎらんぞ |
|
頂点から垂線を下ろしその足をＨとする。 △ＡＢＣのＢＨ＝yとすると、 １３×１３ーｙ×ｙ＝１５×１５ー(１４ーｙ)×(１４ーｙ) これを解くとｙ＝５ 高さはＡＨなので ＡＨ×ＡＨ＋５×５＝１３×１３ これを解いてＡＨ＝１２ 従って△ＡＢＣ＝１４×１２÷２＝８４ｃ㎡ |