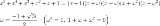
�{������
���w���ӂ��Εۊnj� [�߂�]
|
x+1 x^5-x^4+x^3-x^2+x-1 ���Z�B |
|
(x - e^��i/3)(x - e^2��i/3)(x - e^��i)(x - e^4��i/3)(x - e^5��i/3) |
|
�������݂������l�ɂ���č폜����܂��� |
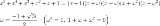 �{������ |
|
x^5+x^4+x^3+x^2+x+1 =x^4(x+1)+x^2(x+1)+(x+1) =(x^4+x^2+1)(x+1) =(x^4+2x^2+1-x^2)(x+1) ={(x^2+1)^2-x^2}(x+1) =(x^2+x+1)(x^2-x+1)(x+1)�@������ł͕s�\�� �����P���̉ߋ���Ɏ����悤�Ȃ̖����������H �ux�̌W�����L���W���܂Łv�̏������L�ژR�ꂾ�������� �����͏�L�ł͂Ȃ������Ƃ��� |
|
��w�����Ȃ�����������Ƃ��A���͗L�����Ȃ낤���ǂ� |
|
> ��w�����Ȃ�����������Ƃ��A���͗L�����Ȃ낤���ǂ� ����Ȃ킯�ˁ[���� |
|
x+1/x=t |
|
�������݂������l�ɂ���č폜����܂��� |
|
�~�@x�͗L���� ���@x�̌W���͗L���� |
|
�������āA(1-x^6)/(1-x)����ˁH �ł͉��p��� 6x^5+5x^4+4x^3+3x^2+2x+1��������������B |
|
���O�͉��������Ă���� |
|
>6x^5+5x^4+4x^3+3x^2+2x+1��������������B =(x^6+x^5+x^4+x^3+x^2+x+1)' =((x^7-1)/(x-1))' =(6x^7-7x^6+1)/(x-1)^2 �Ƃ������Ƃł��傤���B |
|
>>No.89882 ���̒ʂ肾���ǁA������X�Ɉ������������ (1-x^6(7-6x))/(1-x)^2���ĂȂ�B �����ʼn��ɁAv=1-x �Ƃ����ꍇ�A�㎮��(1-x^6(1+6v))/v^2�ƂȂ�B ���܂ł̂��܂Ƃ߂�ƁA �@1+ x+ x^2+ x^3+ x^4+�E�E�E+x^(n-1) = (1-x^n)/v �A1+2x+3x^2+4x^3+5x^4+�E�E�E+nx(n-1) = (1-x^n(1+v))/v^2 �ƂȂ���ǁA���̌� �B1+3x+ 6x^2+10x^3+15x^4+�E�E�E+��x(n-1) = �� �C1+4x+10x^2+20x^3+35x^4+�E�E�E+��x(n-1) = �� �Ƃ����ꍇ�́A ���Ɓ���A���Ɓ��͕����邩�ȁH |
|
���A���߂��L���C�����܂��B^�������Ă��B ���� ----------------------------------------------------- ���܂ł̂��܂Ƃ߂�ƁA �@1+ x+ x^2+ x^3+ x^4+�E�E�E+x^(n-1) = (1-x^n)/v �A1+2x+3x^2+4x^3+5x^4+�E�E�E+nx^(n-1) = (1-x^n(1+v))/v^2 �ƂȂ���ǁA���̌� �B1+3x+ 6x^2+10x^3+15x^4+�E�E�E+��x^(n-1) = �� �C1+4x+10x^2+20x^3+35x^4+�E�E�E+��x^(n-1) = �� �Ƃ����ꍇ�́A ���Ɓ���A���Ɓ��͕����邩�ȁH |
|
���߂�A����������Ă܂����G�G �A�ɁAn��NjL�������܂��B �r���� ----------------------------------------------------- �@1+ x+ x^2+ x^3+ x^4+�E�E�E+ x^(n-1) = (1-x^n)/v �A1+2x+3x^2+4x^3+5x^4+�E�E�E+nx^(n-1) = (1-x^n(1+nv))/v^2 �B1+3x+ 6x^2+10x^3+15x^4+�E�E�E+��x^(n-1) = �� �C1+4x+10x^2+20x^3+35x^4+�E�E�E+��x^(n-1) = �� |
|
�B��x^k�̌W����(k+1)(k+2)/2 �C��x^k�̌W����(k+1)(k+2)(k+3)/6 �ō����Ă܂����H �������Ƃ���Γ�K������O�K�������g�����Ƃ� ���l�̎菇�ŊȖo�������ȋC�����܂� |
|
�W�����Ă̂́A���⁛�̎��ł��ˁB�����Ă܂���B k=n-1�ƍl����Ƃ����Ȃ�܂��B 20�N�قǑO�ɍH��̎d���ŕK�v�ɂȂ�A�����ň����������ċ��߂܂������A�ォ��w����������ǂ������x�ƋC�Â��܂����E�E�E n���g���Čv�Z����ƁA�B�̌W����n(n+1)/2�ƂȂ�܂����A �w������āA1+2+3+4+5+�E�E�E�����߂�z���x�ƋC�Â��� �y���������o��������܂��B |
|
���������ɐ[�x�������H |
|
�[�x���ĉ�����H���w�ł��߂�A��w�o�ĂȂ�����ŁE�E�E �]�k�����Ǐ�L�̇@�A�B�E�E�E�ɂ��āA20�N�߂����� �ŋ߂ɂȂ��āA���̈�A�̎����܂Ƃ߂�Ɓw�d���g���� �g �x�Ƃ������̂��g���ĕ\�������o����̂ƁA x��0�ɋ߂��ꍇ�͋ߎ������|�A�\�����z�̎��ɂȂ鎖�� �C���t���܂����B �i�呲�ł͂Ȃ��̂ŁA���Ƃł͏K���܂���ł����E�E�E�j |
|
�����������ȂƎv���Ă�낤 |