�����P�H
���w���ӂ��Εۊnj�[�߂�]

|
����
�������݂������l�ɂ���č폜����܂��� |
|
����
���� Name No.79385 13/07/20(�y)01:44:52 No.88350 del �������ݓ����ƌ������܂������H �����A���O����{�l��No.88346�̂悤�Ȕn�����肾���� �^�ʖڂɃ��X���Ă������ł��Ȃ��낤���ǂ� ���߂Ă��̔��x���Ă���͓̂��X���r�ɗ��ł��� �ݓ����u�̂����������Ă��Ƃ��炢�͗������� ��No.79385�͑c���ǂ��H�Εa���ĂȂ��œ�������H |
|
����
>�ݓ����l�Ƃ��Ă͊ʼn߂ł��Ȃ� �ނ���{���ɍݓ����l�Ȃ�ʼn߂ł��邾�� |
|
����
�Ԃ����Ⴏ�̃��X�Ƃ��ƂQ�قǎQ�l�ɂȂ��� �T���N�X |
|
����
>��No.79385�͑c���ǂ��H�Εa���ĂȂ��œ�������H �R�s�y�n���̑c���͖k���N���Εa���ĂĂ����悗 |
|
����
>�R�s�y�n���̑c���͖k���N���Εa���ĂĂ����悗 ���O�͉���{�点�� ���{�l�͈������Ƃ��Ă��������ɁA���ł����u���ꂵ�߂�p�m�炸�̋� �����͓��{�����Ĉȗ������Ɖ䂪�����̗̓y�� �o���Ă��� |
|
����
>�Ԃ����Ⴏ�̃��X�Ƃ��ƂQ�قǎQ�l�ɂȂ��� �Ԃ����Ⴏ�̃��X�Ȃ�Ē��w���x�̓��e ������K�E�X�L������combination���̂Ɗi�D���� �����ɂ�����炵�������Ă�ɉ߂��Ȃ� ����ȗe�Ղ������o���鐔�����Q�l�ɂȂ����Ƃ��肪������悤�ł͖��x����Ă�� |
|
����
>����ȗe�Ղ������o���鐔�����Q�l�ɂȂ����Ƃ��肪������悤�ł͖��x����Ă�� ����Ƃ��e�Ղ������o���ė~�������̂� TeX�ŏ����Ă� |
|
����
���� Name No.79385 12/09/17(��)06:09:27 No.80215 del ������ ���� Name No.79385 12/09/17(��)15:40:15 No.80222 del �܁A�L�`�K�C�����������������ڂ��� �S���L�`�K�C�̖ό��ł��� ���� Name No.79385 12/12/23(��)21:26:22 No.82952 del �o�J�ȃI�}�G �� No.79385�͎��g�̈ӌ��ɑΗ��E�^���悷��҂ɑ��u�L�`�K�C�v�Ă�肷�邱�Ƃɉ��� �u�ꂵ���v�u��������v�̈Ӗ�����c���ł��Ȃ��ݓ��r�炵 |
|
����
No.79385�� ���O�͂�肷���� ���X��x�ꂾ���� |

|
����
>���႟��10�{�ŋ@�e�� �����������v�����邩�ăN�C�Y��������s�J�C�`�ȓ������Ǝv�� ���̑O��No.88220�̈�������ʔ��߂��� |
|
����
�X���b�h�𗧂Ă��l�ɂ���č폜����܂��� |
|
����
�u�����ˁI�v�{�^�����~�����Ȃ��� |
|
����
>�u�����ˁI�v�{�^�����~�����Ȃ��� ������ |
|
����
�R�s�y�n�� ���̃X���ɂ̓��X�����Ȃ��� �����r�炵�ȃJ�X |
|
����
�F���y�������ɂ킿��킿�����Ă镵�͋C�����ŋC���������Ȃ��Ē��X����ꂽ���Ȃ��͐S�̕a�C �c�����ɂ��̌��������� |
|
����
�O�{�@���@�Ⓚ |
|
����
�������݂������l�ɂ���č폜����܂��� |
|
����
>�O�{�@���@�Ⓚ ����͂��Ȃ� >�����������͂����ɐ����ƈႤ�������o�������ʔ��� �����Ă��Ȃ��H |
|
����
>���႟��10�{�ŋ@�e�� ��������������ǁA�т�5�Ń����S�Ƃ��C������8���ׂďĂ��݂Ƃ��A�p�^�[���������Ⴄ�Ƃǂ����Ȃ��ċC������B ���悤�ɂ���Ắu����Ə����ăT���o�v�����u�������Ń��b�N�v�����u�o����4���ׂĎ��q���v�����u����9���ׂĒn���v�����A�ǂ��Ƃł��Ȃ�B ��������u�сv�Ƃ����������X���āu�ԗցi�߂̗сj�v�Ƃ��㉺�t�ɂ������ƕ��ʂ̌�����ׂāu�����v�Ƃ����������Ђ˂���̂ق����l�I�ɂ͍D���Ȃ��ǁB ������ւ�͐l�ɂ�邩�B |

|
����
�}���K�ł킩�镨�� �͊w�� [�P�s�{] http://www.amazon.co.jp/%E3%83%9E%E3%83%B3%E3%82%AC%E3%81%A7%E3%82%8F%E3%81%8B%E3%82%8B%E7%89%A9%E7%90%86-%E5%8A%9B%E5%AD%A6%E7%B7%A8-%E6%96%B0%E7%94%B0-%E8%8B%B1%E9%9B%84/dp/4274066657 |

|
����
����͂ݏo���S�{�ōs���邪 ���P�̌ÓT���̌ÓT�ł��� |
|
����
����ʔ������ �A�n�̌��Ƃ����� |
|
����
���x�v������ >��M�����̒����l�{ �Ă����\���Ɉ�a�� |
|
����
>�Ă����\���Ɉ�a�� �ǂ������\����������ǂ��Ǝv���́H |
|
����
>�ǂ������\����������ǂ��Ǝv���́H �ǂ������������ ��������Ȃ��Đ����̕��������C�����邯��.. |
|
����
>�ǂ������\����������ǂ��Ǝv���� 1 �̒�����C�ӂ� 3 �ӏ��܂�Ȃ��č��ꂽ�u�܂���v�ɁA 9 ���� 2�~2 �̊i�q�_�ߍ��ނ��Ƃ��ł��邩�H |
|
����
>��������Ȃ��Đ����̕��������C�����邯��.. �����͏�Ɂu��M�����v�Ȃ���u��M�����̐����v�Ȃ�R�{�ŕK�v�\�� ���Ďw�E�ɂ͂ǂ���������́H >1 �̒�����C�ӂ� 3 �ӏ��܂�Ȃ��č��ꂽ�u�܂���v�ɁA >9 ���� 2�~2 �̊i�q�_�ߍ��ނ��Ƃ��ł��邩�H 1 �̒�����C�ӂ� 3 �ӏ��܂�Ȃ��č��ꂽ�u�܂���v�́A 9 ���� 2�~2 �̐����i�q�_�ߍ��܂��邱�Ƃ��ł��邩�H �ł����̂ł́H |
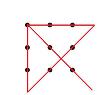
����
 �����P�H |
|
����
4*4��16�̓_���ƒ������{�H 5*5��25�̓_���ƁH n*n�̓_���ƁH |
|
����
���[�����̂ӂ�ӂ튴���Č��H �Ƃ낯��������ő̂������Ⴄ�H ��L����ɓ���āA�H�ׂ� �����̃}�e���A���Ö@��3��J��Ԃ� ��L�@�o�L ���������Â��̃u���E�j�[ �ꔭ�������X�^�[�E�������Â����`���R�u���E�j�[�ɂȂ��ēo��B �Â��Ă��������ɍ��̈ꌂ!? ��L����ɓ���āA�H�ׂ� �����̃}�e���A���Ö@��3��J��Ԃ� ��L�@�o�L |
|
����
���X���C���O�~ �X���C�����O�~�ɂȂ��Ă����ꂽ�I �Ȃ�ƃX���C�����������܂��āc �L���O�X���C���p�b�P�[�W�ɂȂ����I ��L����ɓ���āA�H�ׂ� �����̃}�e���A���Ö@��3��J��Ԃ� ��L�@�o�L ����ɂႭ�[���[ http://recipe.search.yahoo.co.jp/search?rkf=2&p=%E3%81%93%E3%82%93%E3%81%AB%E3%82%83%E3%81%8F%E3%82%BC%E3%83%AA%E3%83%BC&ei=UTF-8 ��L����ɓ���āA�H�ׂ� �����̃}�e���A���Ö@��3��J��Ԃ� ��L�@�o�L |
|
����
����ɂႭ�[���[���ӂ��� http://recipe.search.yahoo.co.jp/search?rkf=2&p=%E3%81%93%E3%82%93%E3%81%AB%E3%82%83%E3%81%8F%E3%82%BC%E3%83%AA%E3%83%BC&ei=UTF-8 ��L����ɓ���āA�H�ׂ� �����̃}�e���A���Ö@��3��J��Ԃ� ��L�@�o�L �O�~���ӂ��� http://recipe.search.yahoo.co.jp/search?rkf=2&p=%E3%82%B0%E3%83%9F&ei=UTF-8 ��L����ɓ���āA�H�ׂ� �����̃}�e���A���Ö@��3��J��Ԃ� ��L�@�o�L |
|
����
���[�����e�B���~�X �@ ���[�����̂ӂ�ӂ튴���Č��H �Ƃ낯��������ő̂������Ⴄ�H ��L����ɓ���āA�H�ׂ� ����3��J��Ԃ� ��L�@�o�L |
|
����
���������Â��̃u���E�j�[ �ꔭ�������X�^�[�E�������Â����`���R�u���E�j�[�ɂȂ��ēo��B �Â��Ă��������ɍ��̈ꌂ!? ��L����ɓ���āA�H�ׂ� ����3��J��Ԃ� ��L�@�o�L ���X���C���O�~ �X���C�����O�~�ɂȂ��Ă����ꂽ�I �Ȃ�ƃX���C�����������܂��āc �L���O�X���C���p�b�P�[�W�ɂȂ����I ��L����ɓ���āA�H�ׂ� ����3��J��Ԃ� ��L�@�o�L |
|
����
����ɂႭ�[���[ http://recipe.search.yahoo.co.jp/search?rkf=2&p=%E3%81%93%E3%82%93%E3%81%AB%E3%82%83%E3%81%8F%E3%82%BC%E3%83%AA%E3%83%BC&ei=UTF-8 ��L����ɓ���āA�H�ׂ� ������3��J��Ԃ� ��L�@�o�L |
|
����
�G���t�E�����C���� �y�X�p�[�N�����O���C���{�J�V�X�{�J�V�X�z�C�b�v�z�L�[�������C�����i�J�V�X�ƃX�p�[�N�C���O���C���j�ɁA�ق�̂� �_���ς��J�V�X�̃z�C�b�v������������e�p�̃G���t�̂悤�ɁB ��L����ɓ���āA�H�ׂ� ������3��J��Ԃ� ��L�@�o�L |

|
����
�������݂������l�ɂ���č폜����܂��� |
|
����
�������݂������l�ɂ���č폜����܂��� |
|
����
�Ƃ肠������ 0<a<1 ����AC:a(x-(-5))-(y-25a)=0 ����BC:(x-5)+a(y-25a)=0 �_C(5��,5a(��+6))�@��=(1-a^2)/(1+a^2) ��ABC=(1/2)*10*[5a(��+6)-25a]=20 2a^2-5a+2=0�@a=1/2,2 0<a<1���a=1/2 �˓_C(3,33/2) �@ �Ȑ�:y=(1/2)x^2 �@ ����AC:y=(1/2)x+15 �_D(6,18) �����CD=3��5/2 |
|
����
C����AB�ɐ������낵�Ă��̑���H�Ƃ��� ��ABC=20�@AB=10 ������ CH=4 ���ƎO�����g���ā@BH=2 �@AH=10-BH=8 ����ā@����AC�̌X��=1/2 |
|
����
10*a/(a^2+1)=4 a^2<1 a=1/2 �ȉ��� |
|
����
�������݂������l�ɂ���č폜����܂��� |
|
����
>���ƎO�����g���ā@BH=2 �����ڂ��� |
|
����
(�P)����No.88162 ���l�A�b�g���S�A�`�a�Ƃ����̌�_ �@�@���d�Ƃ���ƁA�b�d���T�ŗ�̂R�F�S�F�T�̒��p�O�p�` �@�@���ł��A�d�g���R�ƕ�����܂��B �@�@�����b�g���`�g���S��(�T�{�R)���P�^�Q�ƂȂ�܂��B (�Q)�͎O�����̒藝���g�����������ł��ˁB���͂R��T�^�Q �@�@�ł��B�F����̐��w�͂͑f���炵���ł��B |
|
����
�i2�j�̉��� 3��(5/4)�@ �ȋC���������ǁA�A�A �Ȃ�ł݂�� 3��(5/2) �ɂȂ��Ă�H |
|
����
����͒p�������� |

|
����
�������݂������l�ɂ���č폜����܂��� |
|
����
�v����ɖ�������͂ł��� dx �Ƃ����L������Ȃ��Ė������̐��Ƃ��Ĉ����� ��͊w�����̂ł� ���ۂ̉��p�Ƃ��ẮA�m����͂ɗ��p����鎖�������ł� ��dx >> dx (��dx )�E(��dx ) = dx �ƌ��������ŁA�m���ϐ��i��dx �̃I�[�_�[�j�� ���ʂ̐��݂����Ɉ��������\�ɂȂ�܂� |
|
����
>No.88196 ���ӂ��܂� �Ȃ�ق�wiki�ł�����Ɠǂ������Ɛ�(�܂��͕�)�̖�����𐔂Ƃ��Ĉ����ׂɖ����̌��������镪�삩�ȂƎv�����̂ł����Ⴄ�悤�ł��� �{��ǂ������ƉF��(universe)�Ƃ�X�̋�͂Ƃ����O�̓��}��������̂ł��� �����܂��܂��~���������悤�Ńt�B���^�[�̊T�O��c�����邽�߂ɂ́i�m���j���x�����Ȃ��Ƃ����Ȃ��̂��ȂƎv���܂��� |
|
����
>�t�B���^�[�̊T�O��c�����邽�߂ɂ́i�m���j���x�����Ȃ��Ƃ����Ȃ��̂��ȂƎv���܂��� ��Ȃ��Ƃ͂Ȃ��B���x�_�ȑO�̏W���ʑ��ŕK�R�I�ɐg�ɕt���B |
|
����
>��Ȃ��Ƃ͂Ȃ��B���x�_�ȑO�̏W���ʑ��ŕK�R�I�ɐg�ɕt���B �����Ȃ�ł��� �t�B���^�[�̒�`���Ȃ�ƂȂ���-�W���̂̂���Ǝ��Ă����̂� �����ǂ�������(�W��)��͊w�͂��̂ɂ��Ă��Ȃ��Ƃ����܂����� |

|
����
�I�[�X�g�����A��R �u���̐������������l�����̗p������������܂��v �� ���A�Ő������������o�������� �� �u�ŏ��Ɍ��� �������Ă��ꂽ�s��Reddit���[�U�[�����ӂ���B �N���������A�܂��ɂ���ꂪ���߂Ă����ނ̐l�ނ��v |
|
����
����͒p�������� |

|
����
�����͑f�ޖ��ɕ����āA���̌㍬����B �����͉��w�Ȃ̂��B |
|
����
>�����͑f�ޖ��ɕ����āA���̌㍬����B �����Ȃ��Ⴂ���Ȃ��f�ނĉ��A���H |
|
����
>�����Ȃ��Ⴂ���Ȃ��f�ނĉ��A���H ��������e���ʂɂ���ĈႢ������̂ŕ����邯�� �����Ɣ���Ղ��̂̓X�p�C�X��_�V�Ȃǂ̒��������� ��ԒP���Ȃ��͉̂� |
|
����
>�����Ɣ���Ղ��̂̓X�p�C�X��_�V�Ȃǂ̒��������� >��ԒP���Ȃ��͉̂� �f�ނɒ������͓���낤 |
|
����
>�����Ȃ��Ⴂ���Ȃ��f�ނĉ��A���H �̒ʂ肪�������̎ϕ��ꂵ�₷�����̐F���ڂ�₷�����̂��낢�날�邾�낤 |
|
����
�������݂������l�ɂ���č폜����܂��� |
|
����
�ŏ����獬�����ĂȂ����̂��ǂ�����ĕ�����́H �Ƃ�������ŕ������̂��� >�����Ɣ���Ղ��̂̓X�p�C�X��_�V�Ȃǂ̒��������� >��ԒP���Ȃ��͉̂� ��������������܂����̗������o���̂� |
|
����
����A�܂��C����C���Ƌ��Ɖ������ �����Ēn�k�����蕪�����V�R�E���������āc �i���j �ŏł��ڂ��t������ł������� |
|
����
�E�B�W���Ղ��Ǝv���� |
|
����
�Ȃq���I����Ȃ��悤�� |

|
����
��w�@�����i���ɏC�m�j�̉Ȗڂ̕M�L�����́A�ǂ��炩�Ƃ����Ƒ�w�ŏK�������Ƃ��o���Ă��邩���m�F���鑤�ʂ������ł� �������@���̉Ȗڂ̕M�L�����œ_�����ĂȂ��l�́A����������C�͂��Ȃ��Ƃ������ƂŐU�������ޗ��ɂȂ�܂� �M�L�����Ɩʐڎ����Ƃ̊Ԃɂ����Ɖp���ɖڂ�ʂ��āA���������ǂ̂��炢�ł��Ă��邩�m�F���āA�ʐڎ��ɋC�ɂȂ����Ƃ�������ɒ��ڕ����Ă݂āA�ǂ������ԓ������邩�ŗ��_�I�ɗ������Ă��邩�ۂ��f���܂� �ǂ��炩�Ƃ����ƕM�L���������ʐڎ����≞�发�ޒ��̌��݂̌����̊T�v�̕����d�����܂��̂ŁA�M�L�������������炢�����Ă��A�ʐڂŌ����҂Ƃ��Ă̑f�������肻���Ȑl��I�т܂� |
|
����
�@�̓����ŁA�M�L�����d���̂Ƃ�����Ă���́H ���ʂ͖ʐڂƃR�l�Ō��߂�͂������� |
|
����
>�@�̓����ŁA�M�L�����d���̂Ƃ�����Ă���́H ���̒m�����ł͖��� �P�Ȃ�_��蒎�͌����Ɍ����Ȃ����� |
|
����
�_���z���Ȃ�Č��\����ĂȂ����� |
|
����
>�M�L�������������炢�����Ă��A�ʐڂŌ����҂Ƃ��Ă̑f�������肻���Ȑl��I�т܂� �M�L�����ŗ��������͑��������������Ă��Ƃ��E�E�E |
| [0] [1] [2] [3] |